机器之心报道
编辑:杜伟、陈萍@H_404_4@
来自博洛尼亚大学等机构的物理学家利用人工智能,将一个需要 10 万个方程的量子问题,压缩为只需 4 个方程的小任务,这项研究于近日发表在《物理评论快报》上。
相互作用的电子在不同能量和温度下表现出多样的独特现象,假如我们对其周围环境进行改变,它们又会出现新的集体行为,例如自旋、配对波动等,然而处理电子之间的这些现象还存在很多困难。很多研究者使用重整化群(Renormalization Group, RG)来解决。
在高维数据背景下,机器学习 (ML) 技术和数据驱动方法的出现在量子物理中引发了研究者巨大的兴趣,到目前为止,ML 思想已被用于电子系统的相互作用。
本文中,来自博洛尼亚大学等机构的物理学家利用人工智能,将一个迄今为止需要 10 万个方程的量子问题,压缩为一个只需 4 个方程的小任务,而所有这些都在不牺牲准确率的情况下完成,这项研究于近日发表在《物理评论快报》上。

论文地址:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.136402
该研究的第一作者、博洛尼亚大学助理教授 Domenico Di Sante 表示:我们将这个浩大的工程耦合在一起,之后使用机器学习浓缩成一个手指都能数得过来的任务。

Domenico Di Sante
这项研究涉及这一问题,即电子在网格状晶格上运动时动作是怎样的。根据已有的经验,当两个电子占据同一晶格点阵时,它们就会产生相互作用。这一现象可以称为 Hubbard 模型,其是有些材料的理想化设置,基于此,科学家能够了解电子行为如何产生物质相,例如超导性,电子在没有阻力的情况下流过材料。在将新方法应用于更复杂的量子系统之前,该模型还可以作为新方法的试验场。
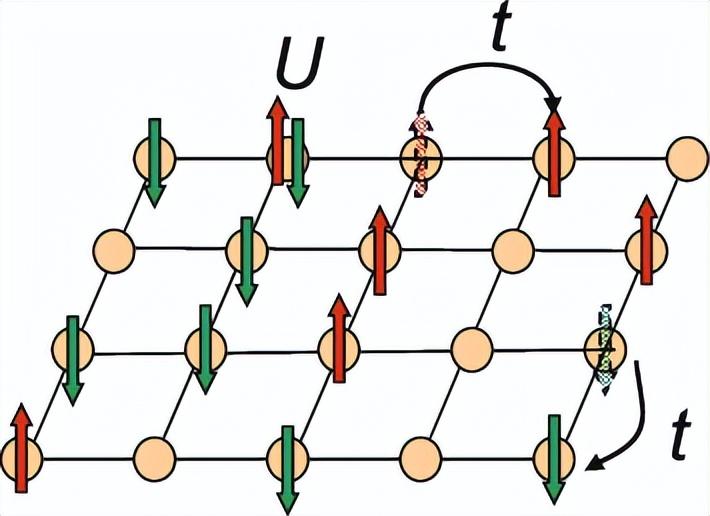
二维 Hubbard 模型示意图。
Hubbard 模型看似简单,但即使是使用尖端计算方法处理少量的电子,也需要强大的算力。这是因为当电子相互作用时,电子之间就变成了量子力学纠缠问题:即使电子所处晶格的位置相距很远,也不能单独处理这两个电子,所以物理学家必须同时处理所有电子,而不是每次只处理一个电子。电子越多,量子力学纠缠就会越多,计算难度就会成倍增加。
研究量子系统的一个常用方法是重整化群。作为一种数学装置,物理学家用它来观察一个系统的行为,比如可以用来观察 Hubbard 模型。遗憾的是,一个重整化群记录了电子之间所有可能的耦合,这些耦合可能包含成千上万、数十万甚至数百万个需要求解的独立方程。最重要的是,方程很复杂:每个方程都代表一对相互作用的电子。
Di Sante 团队想知道他们是否可以使用一种称为神经网络的机器学习工具来使重整化群更易于管理。
就神经网络而言,首先,研究者使用机器学习程序对全尺寸重整化群建立连接;然后神经网络调整这些连接的强度,直到它找到一个小的方程集,生成与原始的、超大的重整化群相同的解。最后得出四个方程,即使只有四个,该程序的输出也捕捉到了 Hubbard 模型的物理性质。
Di Sante 表示:「神经网络本质上是一台能够发现隐藏模式的机器,这一结果超出了我们的预期。」
训练机器学习程序需要大量的算力,因而他们花费了数周的时间才完成。好消息是,现在他们的程序已经开始投入使用,稍微调整就能解决其他问题,而无需从头开始。
在谈到之后的研究方向时,Di Sante 表示需要验证新方法在更复杂的量子系统上的效果如何。此外,Di Sante 还表示,在关于重整化群的其他领域中使用该技术也有很大的可能性,例如宇宙学和神经科学。
论文概述@H_404_4@
针对描述了正方形晶体上广泛研究的二维 t-t' Hubbard 模型的功能重整化群(fRG)流特征的尺度相关四顶点函数,研究者执行了数据驱动降维。他们证明在低维潜在空间中基于神经常微分方程(NODE)求解器的一个深度学习架构能够高效学习描述 Hubbard 模型各种磁性和 d-wave 超导状态的 fRG 动力学。
研究者进一步提出了动态模式分解分析,它能够确认少数模式确实足以捕获 fRG 动力学。研究证明了使用人工智能提取相关电子四顶点函数的紧凑表示的可能性,这是成功实现尖端量子场理论方法并解决多电子问题的最重要目标。
fRG 中的基本对象是顶点函数 V(k_1, k_2, k_3),在原则上需要计算和存储三个连续动量变量组成的一个函数。通过研究特定的理论模式,二维

Hubbard 模型认为这与 cuprates 以及广泛的有机导体相关。研究者表明,较低的维数表示可以捕获高维顶点函数的 fRG 流。
Hubbard 模型的 fRG 接地状态。研究者考虑的微观哈密顿量(Hamiltonian)如下公式(1)所示。

Hubbard 模型的 2 粒子特性通过温度流的一环(one-loop)fRG 方案进行研究,其中

的 RG 流如下公式(2)所示。
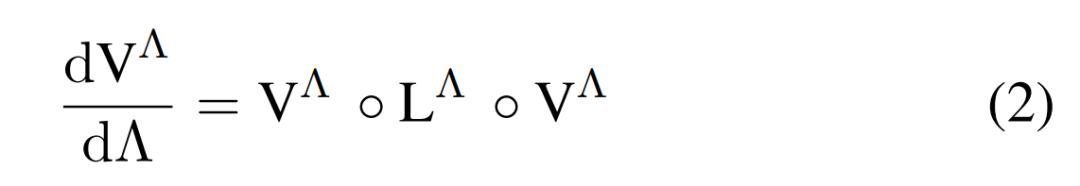
下图 1 a)为 2 粒子顶点函数 V^Λ的一环 fRG 流方程图解表示。

接下来看深度学习 fRG。如下图 2 b)所示,通过在 fRG 流趋向强耦合以及一环近似分解之前检查 2 粒子顶点函数的

耦合, 研究者认识到它们中的很多要么保持边缘状态要么在 RG 流下变得不相关。
研究者在基于适合当前高维问题的参数化 NODE 架构实现灵活的降维方案,该方法如下图 2 a)所示,重点关注深度神经网络。

下图 3 展示了在潜在空间的 fRG 动力学过程中,三个统计上高度相关的潜在空间表示z 作为 NODE 神经网络的学得特征。

更多细节内容请参阅原论文。
原文链接:https://phys.org/news/2022-09-artificial-intelligence-equation-quantum-physics.htm






