1. 大数乘法
在算法中有这么一道经典题:大数乘法。题意
以字符串的形式读入两个数字,编写一个函数计算它们的乘积,以字符串形式返回。(字符串长度不大于10000,保证字符串仅由'0'~'9'这10种字符组成)
示例
输入:"456","123"
返回值:"56088"
说明:456*123=56088
2. 乘法运算规则
按照我们从小学习的乘法运算规则可知:两个数相乘时,可以用其中一个数的每一位与另一个数相乘,然后把相乘结果相加即可得出运算结果。大致如下图所示: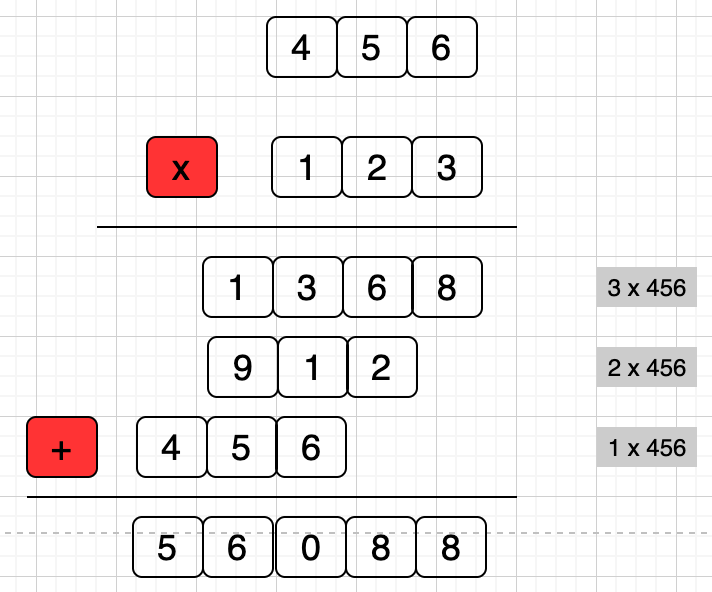
但是,如果把这个运算规则映射到代码中,你会怎么写呢?
从现在开始,给你20分钟的时间写出一个实现算法(20分钟是字节跳动在算法面试时要求的作答时间)。
我猜,此时你会处于两种结果的叠加态:
你奋笔疾书,用片刻就实现了算法。
你边抓耳挠腮,边对面试官漏出尴尬的微笑。
3. 算法实现思路
约定:用m、n分别表示num1、num2两个数字的长度,且它们均不为0。
规则:
num1、num2的乘积结果最长为m+n位对于任意的0≤i<m 和 0≤j<n,num[i]×num [j]的结果位于最终值得[i+j+1]位至于为什么?规则是有数学证明支持的,不信你试一下

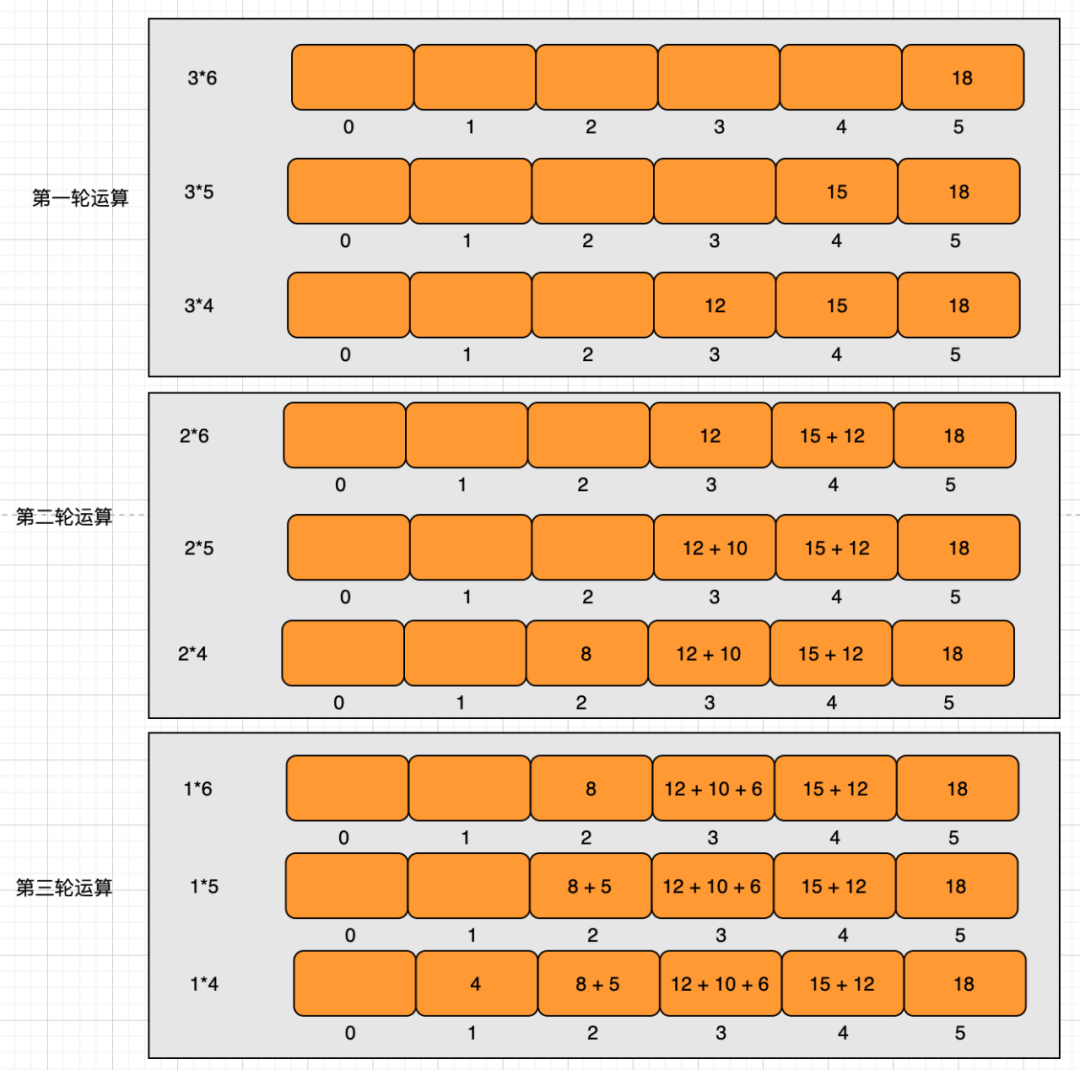

4. Go代码实现大数乘法
根据算法实现思路,使用golang来实现,算法实现如下:/**
* @param t string字符串 第二个整数
* @return string字符串
*/
func solve( s string , t string ) string {
if s == "0" || t == "0" {
return"0"
}
// 两数相乘,最大长度为 m+n
m, n := len(s), len(t)
arr := make([]int, m+n)
for i:=m-1; i>=0; i--{
n1 := int(s[i]-'0')
for j:=n-1; j>=0; j--{
n2 := int(t[j]-'0')
// m的第i位乘以n的第j位,位于最终数组的j+j+1的位置
// 理解这里很重要。i+j+1 可能是一个大于10的数字
// 因为这里存储的是乘积,没向前进位
arr[i+j+1] += n1*n2
}
}
// 处理进位,i的进位位置在i-1位置
for i:= len(arr)-1; i>0; i--{
arr[i-1] += arr[i]/10
arr[i] = arr[i]%10
}
// 如果第0位为0,则需要处理
inx := 0
if arr[0] == 0 {
inx =1
}
res := ""
for i:= inx; i<len(arr); i++{
res += strconv.Itoa(arr[i])
}
return res
}至此,大数乘法已实现完毕。这里想说的是,切记从问题中推导出可以使用程序实现的通用性规则。
5. 参考及算法题出处
力扣-字符串相乘 https://leetcode-cn.com/problems/multiply-strings/牛客网-大数乘法
https://www.Nowcoder.com/practice/c4c488d4d40d4c4e9824c3650f7d5571






