2022杭电多校第四场题解

2022杭电多校第四场

Link with Bracket Sequence II（区间DP）

题意
给定一个长度为$n(1<=n<=500)$的括号序列，括号种类数为$m(1<=m<=10^9+7)$，括号序列中某些位置的括号丢失了。对于第$i$个位置的括号，$a[i]>0$表示左括号，$a[i]<0$表示右括号，$a[i]=0$表示括号丢失。问有多少种填充方案使得整个序列称为一个合法的括号序列，答案对$10^9+7$取模。

分析
根据数据范围可以想到区间DP，接下来考虑如何进行状态表示。
$f[i][j]$表示区间$[i,j]$为合法括号序列且$i$和$j$匹配的方案数，$g[i][j]$表示区间$[i,j]$为合法括号序列的方案数，则有如下状态转移方程。
$$\{\begin{array}{l}f[i][j]=k\ast g[i+1][j-1](k\mathrm{表示}i和j\mathrm{匹配的方案数})\\ g[i][j]=\sum g[i][k]\ast f[k+1][j]\end{array}$$
如果直接用$f[i][j]$表示区间$[i,j]$为合法括号序列的方案数，会导致重复。对于()()()这种情况，在进行合并时，有两种合并方法()|()()和()()|()，上述状态表示方法可以避免重复。时间复杂度$O(n^3)$。

AC代码

typedef long long ll;
const int mod=1e9+7;
const int N=510;
int a[N];
ll f[N][N],g[N][N];

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n,m;
		cin>>n>>m;
		for(int i=1;i<=n;i++) cin>>a[i];
		if(n&1)
		{
			cout<<0<<endl;
			continue;
		}
		memset(f,0,sizeof(f));
		memset(g,0,sizeof(g));
		for(int i=1;i<=n+1;i++) g[i][i-1]=1;
		for(int k=2;k<=n;k++)
		{
			for(int i=1;i+k-1<=n;i++)
			{
				int j=i+k-1;
				ll sum=0;
				if(!a[i]&&!a[j]) sum=m;
				else if((!a[i]||!a[j])&&(a[i]>0||a[j]<0)) sum=1;
				else if(a[i]>0&&a[i]==-a[j]) sum=1;
				f[i][j]=sum*g[i+1][j-1]%mod;
			}
			for(int i=1;i+k-1<=n;i++)
			{
				int r=i+k-1;
				for(int j=i-1;j<r;j+=2) //优化，合法括号序列区间长度为偶数
				{
					g[i][r]=(g[i][r]+g[i][j]*f[j+1][r]%mod)%mod;
				}
			}
		}
		cout<<g[1][n]<<endl;
	}
	return 0;
}

Link with Equilateral Triangle（思维）

题意
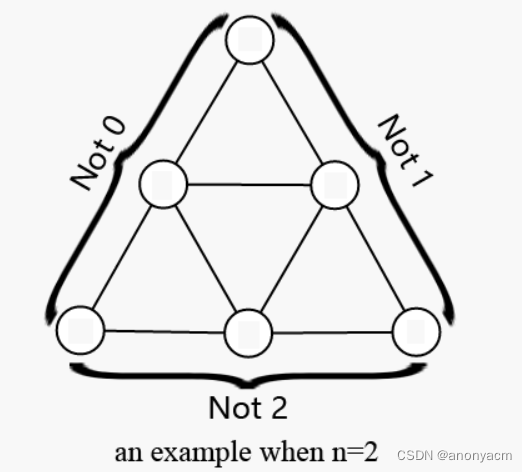
有一个边长为$n$的等边三角形(equilateral triangle)，这个等边三角形包含$n^2$个边长为$1$的等边三角形。每个顶点可以填0、1或2，等边三角形左边的顶点不能填0，右边的顶点不能填1，底部的顶点不能填2，要求每个边长为1的等边三角形点权之和不能是3的倍数。现在给出等边三角形的边长，问在满足上述条件下是否存在一种方案在等边三角形的每个顶点填上数字。

分析
对于一个合法的解，应当满足不存在同时包含0，1，2的三角形，下面证明这样的三角形一定存在。首先，等边三角形的左下角必然是1，右下角必然是0，顶部必然是2，底边不能含有2，则底边上必然有奇数条0-1边，这些边都属于一个小三角形。考虑其他的0-1边，由于不在两个斜边上，其他的0-1边必然属于两个边长为1的等边三角形。因此边长为$n$等边三角形内0-1边的数量的和必然为奇数。但是，假设不存在0-1-2的三角形，则所有等边三角形都必然包含0条或2条的0-1边，产生了矛盾。因此一定存在0-1-2的三角形。

AC代码

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n;
		cin>>n;
		cout<<"No"<<endl;
	}
	return 0;
}

BIT Subway（分段函数 模拟）

题意
DLee买了$n$张票，每张票的价格为$a_i(1<=a_i<=200)$。现在对票价有一个优惠方案，如果当前票价总和大于等于$100$，之后购买的票只需支付$0.8\times$票价，如果当前票价总和大于等于$200$，之后购买的票只需支付$0.5\times$票价。购买票时不能对票价进行拆分，但DLee却认为票价可以拆分，输出两种情况下的票价。

分析
DLee的价格实际上是一个关于总原票价$x$的分段函数：

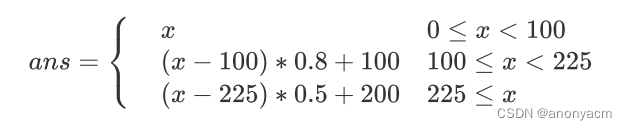
真实票价直接模拟即可。

AC代码

const int N=1e5+10;
int a[N];
int n;

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		cin>>n;
		for(int i=1;i<=n;i++) cin>>a[i];
		double sum1=0,sum2=0;
		for(int i=1;i<=n;i++) sum1+=a[i];
		if(sum1>100&&sum1<=225) sum1=100+(sum1-100)*0.8;
		else if(sum1>225) sum1=200+(sum1-225)*0.5;
		for(int i=1;i<=n;i++)
		{
			if(sum2>=200) sum2+=a[i]*0.5;
			else if(sum2>=100) sum2+=a[i]*0.8;
			else sum2+=a[i];
		}
		cout<<fixed<<setprecision(3)<<sum1<<" "<<sum2<<endl;
	}
	return 0;
}

Climb Stairs（贪心 数据结构）

题意
一个建筑有$n$层楼梯，每层楼梯都有一个怪兽，怪兽的生命值为$a_i(1<=a_i<=10^9)$。DLee位于地面(第0层)，攻击力为$a_0$，他每次可以向上跳不超过$k$层楼梯或者向下走一层楼梯。DLee不能去怪兽生命值严格大于他攻击力的楼层也不能去他访问过的楼层。DLee每打败一个怪兽就可以吸收怪兽的生命值加到自己的攻击力，问DLee是否可以打败所有怪兽。

分析
假设当前所在楼层为$x$，DLee可以到达的楼层为$[l,r]$，其中$l=x+1$，$r=x+k$。在$[l,r]$中要找到一个楼层$y$满足DLee到达$y$后可以从$y$到达$l$，并且DLee到达$[l,r]$中任何一个满足条件的$y$都是最优的。DLee到达$y$后可以一直下楼到$l$的条件是DLee当前攻击力大于等于$max(a[i]-(sum[y]-sum[i-1]))(l<=i<=y)$，其中$a[i]$和$sum[i-1]$是定值，可以用数据结构维护。具体实现时可以从$l$到$r$找到第一个满足条件的$y$，之后更新$l$和$r$，如果找不到就无解。时间复杂度$O(nlog(n))$。

AC代码

typedef long long ll;
const int N=1e5+10;
ll a[N],sum[N];
int n; 
struct Segment_Tree {
	#define lc(x) (x<<1)
	#define rc(x) (lc(x)|1)
	ll tr[N<<2];
	void pushup(int p) { tr[p]=max(tr[lc(p)],tr[rc(p)]); }
	void build(int p,int l,int r) {
		if(l==r) { tr[p]=a[l]+sum[l]; return; }
		int mid=(l+r)>>1;
		build(lc(p),l,mid);
		build(rc(p),mid+1,r);
		pushup(p);
	}
	ll query(int p,int l,int r,int x,int y) {
		if(x<=l&&r<=y) return tr[p];
		int mid=(l+r)>>1;
		ll mx=0;
		if(x<=mid) mx=max(mx,query(lc(p),l,mid,x,y));
		if(y>mid)  mx=max(mx,query(rc(p),mid+1,r,x,y));
		return mx;
	}
}seg;

bool check(int l,int r,ll x)
{
	ll mx=seg.query(1,1,n,l,r);
	mx=max(0ll,mx-sum[r]);	
	return mx<=x;
}

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int a0,k;
		cin>>n>>a0>>k;
		for(int i=1;i<=n;i++) cin>>a[i],sum[i]=sum[i-1]+a[i];
		bool flag=true;
		int l=1,r=min(k,n);
		seg.build(1,1,n);
		while(true)
		{
			int x=-1;
			for(int i=l;i<=r;i++)
			{
				if(check(l,i,a0))
				{
					x=i;
					break;
				}
			}
			if(x==-1)
			{
				flag=false;
				break;
			}
			a0+=sum[x]-sum[l-1];
			if(x==n) break;
			r=min(n,l+k),l=x+1;
		}
		if(flag) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
	}
	return 0;
}

Link is as bear（思维 线性基）

题意
给定一个长度为$n$的数组，每次选择一个区间$[l,r](l<=r)$，使$a[i]=xor(l,r)(i\in [l,r])$，其中$xor(l,r)=a_l\oplus a_{l+1}\oplus \dots \oplus a_r$。要求最终数组中所有元素相同，求相同值的最大值。题目保证$\exists x,y(x\ne y)$使得$a_x=a_y$。

分析
问题完全等价于给定$n$个数，从中选一些数，使得这些数的异或和最大，这是线性基的模板题。
下面证明这两个问题等价：
用1表示要选择的数字，0不是不选的数字，则原数组可表示为01序列。分情况讨论：
（1）序列中出现两个连续的0，假设所在位置为$i$和$i+1$，通过两次选择$[i,i+1]$，将这两个数字变为0
（2）序列中出现两个连续的1，以110为例，假设这三个数的位置为$x$、$y$、$z$，则通过$[x,y]$、$[y,z]$、$[y,z]$三次操作将序列变为100，且$y$和$z$所在位置的数字值为0
（3）序列中不存在连续两个0/1，即形如10101或01010这两种情况。由于题目保证$\exists x,y(x\ne y)$使得$a_x=a_y$，考虑将序列转化为前两种情况。如果$x$和$y$奇偶性相同，则$x$和$y$要么同时为0，要么同时为1，这样可以保证构造出连续两个0/1；如果$x$和$y$奇偶性不同，$x$和$y$必须一个为0，一个为1，交换$x$和$y$的01状态可以构造出连续两个0/1，因此第(3)种情况可以转化为(1)/(2)

通过上述操作可以保证序列中出现两个连续的0(数值0)，如果要选的数字和两个连续的0相邻可以移动位置，如果不选的数字和0相邻可以变为0，经过若干次变化后整个序列中要选的数字留下，不选的数字变为0，通过选择区间$[1,n]$得到最优解。

下面给出题解证明。

AC代码

typedef long long ll;
const int N=1e5+10;
ll a[N];
int n;

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		cin>>n;
	    for(int i=0;i<n;i++) cin>>a[i];
	    int k=0;
	    for(int i=55;i>=0;i--)
	    {
	        for(int j=k;j<n;j++)
	        {
	        	if(a[j]>>i&1)
	            {
	                swap(a[j],a[k]);
	                break;
	            }
			}
	        if(!(a[k]>>i&1)) continue;
	        for(int j=0;j<n;j++)
	        {
	        	if(j!=k&&(a[j]>>i&1))
				{
					a[j]^=a[k];
				} 
			}
	        k++;
	        if(k==n) break;
	    }
	    ll ans=0;
	    for(int i=0;i<k;i++) ans^=a[i];
	    cout<<ans<<endl;
	}
    return 0;
}