问题描述
预计阅读时间:10分钟
1.单选题(2分)
以下不属于面向对象程序设计语言的是( )。
A.C++
B.Python
C.Java
D.C
解析:C语言并非面相对对象,而是面向过程。
答案:D
2.单选题(2分)
以下奖项与计算机领域最相关的是( )。
A.奥斯卡奖
B.图灵奖
C.诺贝尔奖
D.普利策奖
解析:奥斯卡奖是电影奖,诺贝尔奖是诺贝尔遗嘱里的5个奖,普利策奖是新闻奖,图灵奖是计算机领域的奖项。
答案:B
3.单选题(2分)
目前主流的计算机储存数据最终都是转换成( )数据进行储存。
A.二进制
B.十进制
C.八进制
D.十六进制
解析:计算机将全部信息转换成二进制进行传输。
答案:A
4.单选题(2分)
以比较作为基本运算,在N个数中找出最大数,最坏情况下所需要的最少的比较次数为( )。
A.N^2
B.N
C.N - 1
D.N + 1
解析:最值问题,以第一个数作为初始值,从第二个数开始比较,最坏情况下要比较到序列末尾才能得到最大值,即比较 N-1 次。
答案:C
5.单选题(2分)
对于入栈顺序为a,b,c,d,e的序列,下列( )不是合法的出栈序列。
A.a,b,c,d,e
B.e,d,c,b,a
C.b,a,c,d,e
D.c,d,a,e,b
解析:acb进栈,c出栈,d进栈出栈,之后从栈顶到栈底还有b,a没有出栈,a无法在b之前先出栈。
答案:D
6.单选题(2分)
对于有nn个顶点、mm条边的无向联通图(m>n),需要删掉( )条边才能使其成为一棵树。
A.n - 1
B.m - n
C.m - n - 1
D.m - n + 1
解析:n个顶点的树有n-1条边,需删除 m-(n-1)= m-n+1条边。
答案:D
7.单选题(2分)
二进制数101.11对应的十进制数是( )。
A.6.5
B.5.5
C.5.75
D.5.25
解析:直接计算即可。
答案:C
8.单选题(2分)
如果一棵二叉树只有根结点,那么这棵二叉树高度为1。请问高度为5的完全二叉树有( )种不同形态?
A.16
B.15
C.17
D.32
解析:h=5 的完全二叉树共有 24 个节点,第五层最少1个节点,最多16个节点,因此一共有16种情况。
答案:A
9.单选题(2分)
表达式a*(b+c)*d 的后缀表达式为( ),其中“*”和“+”是运算符。
A.**a+bcd
B.abc+*d*
C.abc+d**
D.*a*+bcd
解析:考察前后缀表达式。表示为( a [ bc +] * ) d *,后缀表达式为 abc+*d*。
答案:B
10.单选题(2分)
6个人,两个人组一队,总共组成三只不区分队伍的编号,不同的组队情况有()种。
A.10
B.15
C.30
D.20
C62×C42×C
解析:排列组合问题。一共有C(6,2)*C(4,2)*C(2,2)种组合方法。但是由于不区分队伍编号,还要除以A(3,3),最终组队情况一共有:15种。
答案:B
11.单选题(2分)
在数据压缩编码中的哈夫曼编码方法,在本质是一种( )的策略。
A.枚举
B.贪心
C.递归
D.动态规划
解析: 哈夫曼编码每次把频率最低的两个节点合并,产生新的节点并放在集合中,删除用来合并的两个节点,重复这个过程直到剩下一个节点为止。每次选择频率最小的两个节点就是贪心的思想。
答案:B
12.单选题(2分)
由1, 1, 2, 2, 3这五个数字组成不同的三位数有( )种。
A.18
B.15
C.12
D.24
解析:枚举法,不同的三位数有:321,322,311,312,211,212,213, 221, 223,231, 232, 112,113,121,122,123,131,132共十八种。
答案:A
考虑如下递归算法,则调用solve(7)solve(7)得到的返回结果为( )。
solve(n)
if n<=1 return 1
else if n>=5 return n*solve(n-2)
else return n*solve(n-1)
A.105
B.840
C.210
D.420
解析:solve(7)=7×solve(5)
= 7×5×solve(3)
=7×5×solve(3)
= 7×5×3×solve(2)
=7×5×3×solve(2)
= 7×5×3×2 ×solve(1)
=7×5×3×2×solve(1)
= 7×5×3×2×1
=7×5×3×2×1
=210
答案:C
14.单选题(2分)
以aa为起点,对右边的无向图进行深度优先遍历,则b、c、d、eb、c、d、e四个点中有可能作为最后一个遍历到的点个数为( )。
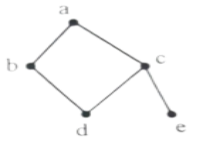
A.1
B.2
C.3
D.4
解析:从a→b方向的遍历:a-b-d-c-e; 从a→c方向的遍历:a-c-e-d-b和a-c-d-b-e。 则最多有两个终点:e和b。
答案:B
15.单选题(2分)
有四个人要从AA点做一条船过河到BB点,船一开始在AA点。该船一次最多可坐两个人。已知这四个人中每个人独自坐船的过河时间分别为1, 2, 4, 8, 且两个人坐船的过河时间为两人独自过河时间的较大者。则最短( )时间可以让四个人都过河到BB点(包括从BB点把船开回AA点时间)。
A.14
B.15
C.16
D.17
解析:和2从 A→B,1从B→A,此时A点有1,4,8 ;
B点有2,所用时间:2+1=3; 4和8从A→B,2从B→A。此时A点有1,2; B点有4,8,所用时间:8+2=10;
最后1和2从A→B,所用时间为2;总时间为3+10+2=15。
答案:B
16.填空题(10.5分)
#include <stdio.h>
int n;
int a[1000];
int f(int x)
{
int ret = 0;
for (; x; x &= x - 1) ret++;
return ret;
}
int g(int x)
{
return x & -x;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
for (int i = 0; i < n; i++)
printf("%d ", f(a[i]) + g(a[i]));
printf("\n");
return 0;
}
•判断题
1)输入的nn等于1001时,程序不会发生下标越界。()
2)输入的 a[i]a[i] 必须全为正整数,否则程序将陷入死循环。()
3)当输入为”5 2 11 9 16 10”时,输出为”3 4 3 17 5”。()
4)当输入为”1 511998”时,输出为”18” 。()
5)将源代码中g函数的定义(13-16行)移到main函数的后面,程序可以正常编译运行。()
•单选题
6)当输入为”2 -65536 2147483647”时,输出为()
1.
A.正确
B.错误
2.
A.正确
B.错误
3.
A.正确
B.错误
4.
A.正确
B.错误
5.
A.正确
B.错误
6.
A."65532 33"
B."65552 32"
C."65535 34"
D."65554 33"
解析:本题考察位运算及进制转换相关知识。
&代表按位与,即将参与运算的两数均转换为二进制后逐位进行与运算。只有当参与运算的对应两位均为1时,结果对应位才为1。例如:8 &11=(1000)211=(1000)2 & (1011)2=(1000)2=8(1011)2=(1000)2=8
对于f(x)f(x):思考二进制中借位过程,本质上是将被借位变为0,并将被借位右侧直至借位者位置的0全部变为1。更具体地,我们可以将xx写成(A)1(B)(A)1(B)形式,B代表nn个0,即A与B中间的1为xx从右向左数第一个1。则x−1x−1将为(A)0(C)(A)0(C)形式,C代表nn个1。参考按位与定义,则xx & (x−1)=(A)0(B)(x−1)=(A)0(B)。所以本质上xx&=(x−1)=(x−1)的作用为将xx的最右侧的1变为0。每次循环会将一个1变为0,循环终止条件为xx变为0,则实际上retret统计的就是xx二进制表示中1的数目。
对于g(x)g(x):返回xx&(−x)(−x)。负数在计算机中的表示为原正数二进制取反后+1。如10的二进制表示为0000 1010,其取反后为1111 0101。11110101+1=1111011011110101+1=11110110。即-10的二进制表示为1111 0110。 不难发现,+1这个行为会导致进位。具体地,+1会将取反后二进制数码中最右端的所有1(由于进位)变为0,并将取反后二进制数码中从右边数第一个0变为1。又由于取反,在原二进制中对应从右边数第一个0的位置的数,实际上就为从右边数的第一个1(右边全为0)。综上可以发现,一个数与他的的相反数在二进制中,从右向左直到第一个1为止都是相同的,而在从右向左数第一个1的左侧,该数与其相反数的每一位二进制数码均相反。因此,xx&(−x)(−x)将得到除了在原数中最右侧的1的位置为1,其余位置全为0的二进制数。
如:0100000001000000 & [−(01000000)]=01000000[−(01000000)]=01000000 & 11000000=0100000011000000=01000000
实际上,由此可得当一个偶数与他的负值相与时结果是能被这个偶数整除的最大的2的nn次幂;当一个奇数与他的负值相与时结果一定是1.
1.aa数组的大小为1000,因此下标为0~999,1001越界
2.f(x)f(x)与在xx为正整数与负整数时均可正常运作,不会进入死循环,错误
3.最后输出为 f(a[i])+g(a[i])f(a[i])+g(a[i]) 形式。当输入5(二进制为101)时:1的个数为2个,则 f(a[i])=2f(a[i])=2;最低位的1表示为1,则g(a[i])=2g(a[i])=2 ;则输出为(2+1=3)(2+1=3). 以此类推…
然而当输入为10(二进制为1010)时, f(a[i])=2,g(a[i])=2f(a[i])=2,g(a[i])=2 ;则输出为(2+2=42+2=4),不应该为5
4.考察进制转换。511998的二进制表示为111 1100 1111 1111 1110,所以f(511998)=16,g(511998)=2f(511998)=16,g(511998)=2,输出18,正确。
5.若要将函数移动至mainmain函数后面,则需要先在mainmain前进行声明,否则不能编译运行。
6.显然硬算相当容易出错,且时间成本很高。观察发现2147483647实际上就是intint的最大值,即231−1231−1。故此f(2147483647)=31,g(2147483647)=1,f(x)+g(x)=32f(2147483647)=31,g(2147483647)=1,f(x)+g(x)=32,因此第二个输出为32,选B
答案:BBBABB
17.填空题(14分)
#include <stdio.h>
#include <string.h>
char base[64];
char table[256];
char str[256];
char ans[256];
void init()
{
for (int i = 0; i < 26; i++) base[i] = 'A' + i;
for (int i = 0; i < 26; i++) base[26 + i] = 'a' + i;
for (int i = 0; i < 10; i++) base[52 + i] = '0' + i;
base[62] = '+', base[63] = '/';
for (int i = 0; i < 256; i++) table[i] = 0xff;
for (int i = 0; i < 64; i++) table[base[i]] = i;
table['='] = 0;
}
void decode(char *str)
{
char *ret = ans;
int i, len = strlen(str);
for (i = 0; i < len; i += 4) {
(*ret++) = table[str[i]] << 2 | table[str[i + 1]] >> 4;
if (str[i + 2] != '=')
(*ret++) = (table[str[i + 1]] & 0x0f) << 4 | table[str[i + 2]] >> ;
if(str[i + 3] != '=')
(*ret++) = table[str[i + 2]] << 6 | table[str[i + 3]];
}
}
int main()
{
init();
printf("%d\n", (int)table[0]);
scanf("%s", str);
decode(str);
printf("%s\n", ans);
return 0;
}•判断题
1)输出的第二行一定是由小写字母、大写字母、数字和”+”、”/”、”=”构成的字符串。()
2.)可能存在输入不同,但输出的第二行相同的情形。()
3)输出的第一行为”-1”。()
•单选题
4)设输入字符串长度为nn,decodedecode函数的时间复杂度为()
5)当输入为”Y3Nx”时,输出的第二行为()
6)当输入为”Y2NmIDIwMjE=”时,输出的第二行为()
1.
A.正确
B.错误
2.
A.正确
B.错误
3.
A.正确
B.错误
4.
A.O(√n)O(√n)
B.O(n)O(n)
C.O(nlogn)O(nlogn)
D.O(n2)O(n2)
5.
A.”csp”
B.“csq”
C.”CSP”
D.“Csp”
6.
A.”ccf2021”
B.”ccf2022”
C.”ccf 2021”
D.”ccf 2022”
解析:难题。缺少相关背景知识的情况下相当考察理解能力。实际上本题是在解码用base64base64加密的一串字符串。Base64Base64就是用来将非ASCIIASCII字符的数据转换成ASCIIASCII字符的一种方法。特别适合在http,mime协议下快速传输数据。也可以用来加密,不过这种方法比较初级。
加密方式:一个charchar在计算机中对应的是8个bit。
比如 'aa' 在计算机中对应的是97,对应的存储内容是0110 0001,占用8个bit。
这样的话,把三个 charchar 对应的 24个 bit 每6个一组变成4个元素,重新编码就达到了加密的目的。
因此解码就是将四个元素变回三个元素。
init()init()函数初始化:basebase下标0~63对应字符ASCIIASCII码A~Z,a~z,0~9,+,/,加密即通过basebase数组进行对应加密。tabletable使用A~Z,a~z,0~9,+,/作为下标,对应0~63,用作解码。字符‘=’对应0,在本题中可以理解为占位符作用。
decode()decode()函数:如上所说,我们的解码方式为将每四个元素变回三个元素。因此循环ii每次+4,一次将四个元素进行解密处理。由于加密过程为将3个8个bit分为4份,每份6 bit

如图所示,我们要还原第一个字符则需要密码的第一个字符的全6 bit与第二个字符的前2 bit;
同理,还原第二个字符需要密码的第二个字符的后4 bit与第三个字符的前4 bit;
还原第三个字符需要密码第三个字符的后2 bit与第四个字符的全6 bit;
接下来来看位运算的具体实现。
还原第一个字符:table[str[i]]<<2∣table[str[i+1]]>>4table[str[i]]<<2∣table[str[i+1]]>>4;
先用tabletable将字符转回数码形式。由于我们需要密码第一个字符的全6 bit与第二个字符的前2 bit,因此我们将第一个密码字符前移2位,相当于为第二个字符的前2 bit腾出空间。然后我们将第二个密码字符右移四位,则得到的就是第二个密码字符的前2 bit且位于一个数码的最右端。接着我们进行一次按位与运算,则这2 bit就刚好填入第一个字符预留出的空间中形成8 bit数码,经过charchar类型强转即可解码为第一个字符。
第二第三个字符的还原同理。特别地,第二个字符的还原中出现了table[str[i+1]]table[str[i+1]] & 0x0f0x0f。0x0f对应二进制的1111,进行&运算的意义为取最低的4位。
1.错误,完全有可能出现其他字符。
2.正确,是有可能的。例如‘a0==a0==’和‘a1==a1==’输出均为‘kk’这是因为‘=’省略了密码字符0与1在后四位上的不同,并不将后4位加入解码。
3.正确。tabletable初始化为0xff,同时table[0]table[0]在此之后并未被赋值。0xff二进制表达为补码11111111,十进制表达即为-1。
4.观察发现decodedecode函数中的循环实际上遍历了整个传入数组,每个字符进行的操作为常数次,因此渐进时间复杂度为O(n)O(n)的
5.模拟程序操作。t[‘Y’]∣t[‘3’]=(24<<2∣55>>4)=01100011=99=‘c’t[‘Y’]∣t[‘3’]=(24<<2∣55>>4)=01100011=99=‘c’
t[‘N’]<<6∣t[‘x’]=01000000∣00110001=113=‘q’t[‘N’]<<6∣t[‘x’]=01000000∣00110001=113=‘q’
6.由于最后有一个‘=’,因此最后四个密码字符实际上还原后为2个字符,因此一共应有3+3+2=83+3+2=8个字符,排除AB。模拟最后一个字符的还原发现还原后为1,故此选C
答案:BAABBC
18.填空题(15.5分)
#include <stdio.h>
#define n 100000
#define N n+1
int m;
int a[N], b[N], c[N], d[N];
int f[N], g[N];
void init()
{
f[1] = g[1] = 1;
for (int i = 2; i <= n; i++) {
if (!a[i]) {
b[m++] = i;
c[i] = 1, f[i] = 2;
d[i] = 1, g[i] = i + 1;
}
for (int j = 0; j < m && b[j] * i <= n; j++) {
int k = b[j];
a[i * k] = 1;
if (i % k == 0) {
c[i * k] = c[i] + 1;
f[i * k] = f[i] / c[i * k] * (c[i * k] + 1);
d[i * k] = d[i];
g[i * k] = g[i] * k + d[i];
break;
}
else {
c[i * k] = 1;
f[i * k] = 2 * f[i];
d[i * k] = g[i];
g[i * k] = g[i] * (k + 1);
}
}
}
}
int main()
{
init();
int x;
scanf("%d", &x);
printf("%d %d\n", f[x], g[x]);
return 0;
}假设输入的xx是不超过1000的自然数,完成下面的判断题和单选题:
•判断题
1)若输入不为”1”,把第12行删去不会影响输出的结果。()
2)第24行f[i * k] = f[i] / c[i * k] * (c[i * k] + 1)中的” f[i]/c[i*k]”可能存在无法整除而向下取整的情况。()
3)在执行完init()init()后,f数组不是单调递增的,但gg数组是单调递增的。()
•单选题
4)initinit函数的时间复杂度为()。
5)在执行完init()init() 后,f[1],f[2],f[3]......f[100]f[1],f[2],f[3]......f[100]中有()个等于2。
6)当输入”1000”时,输出为()。
1.
A.正确
B.错误
2.
A.正确
B.错误
3.
A.正确
B.错误
4.
A.O(n)O(n)
B.O(nlogn)O(nlogn)
C.O(n√n)O(n√n)
D.O(n2)O(n2)
5.
A.23
B.24
C.25
D.26
6.
A.”15 1340”
B.”15 2340”
C.”16 2340”
D.”16 1340”
解析:实际上是一个线性素数筛(或者叫欧拉筛)的代码,同时处理了约数个数与约数和。欧筛在埃筛的基础上每个合数只被它的最小质因子筛一次,以达到不重复的目的。
各个数组作用:
a[]a[]标记质数,若为0则为质数。
b[]b[]存储所有质数。
c[]c[]存储最小质因子个数。
d[]d[]: (p0+p1+…pnump0+p1+…pnum),pp为最小质因子,numnum为pp的个数;
f[]f[]存储约数个数
g[]g[]存储约数和
重要定理与公式:
(1)每一个大于等于2的正整数NN都可以被分解为如下形式:
N=p1a1p2a2...pnanN=p1a1p2a2...pnan
pp为素数。由此可以筛出素数。
(2)一个数NN的约数个数等于分解后所有素因子+1后的积,即
d(N)=(1+a1)(1+a2)...(1+an)d(N)=(1+a1)(1+a2)...(1+an)
由此可以筛出NN的约数个数。筛的过程中保存最小质因子个数c[]c[]。
素数只有一个质因子为其本身,且指数为1,约数个数为2.
题面中若i%k!=0i%k!=0,代表ii中不含kk这个质因子。但i×ki×k中包含一个kk
又我们已知ii的约数个数为f[i]f[i],则i×ki×k的约数个数即为f[i]×2f[i]×2,(比ii多了一个质因数kk,其指数为1)
又因为从小到大枚举,所以kk必然为i×ki×k的最小质因子,有一个,所以记c[i×k]=1c[i×k]=1
若i%k==0i%k==0,那么ii中至少包含一个kk,且由于从小到大枚举,kk必然为ii的最小质因子。
这时,i×ki×k的最小值因子个数就比ii多1,即c[i×k]=c[i]+1c[i×k]=c[i]+1。则i×ki×k的约数个数计算公式和i完全一样,除了ii中的(1+a11+a1)项变为(1+a1+11+a1+1)。
因此有f[i×k]=f[i]/c[i×k]×(c[i×k]+1)f[i×k]=f[i]/c[i×k]×(c[i×k]+1);
(3)一个数NN的约数和等为:
sd(N)=(1+p1+p12+...+p1a1)(1+p2+p22+...+p2a2)...(1+pn+pn2+...+pnan)sd(N)=(1+p1+p12+...+p1a1)(1+p2+p22+...+p2a2)...(1+pn+pn2+...+pnan)
由此可以筛出NN的约数和。筛的过程中保存最小素因子那一项的和d[]d[]。
观察公式,实际上和约数个数公式相当相似。筛法推导过程也与约数筛法基本一致。
1.正确。当输入不为1时,int k = b[j] 中kk的取值不会是1,那么forfor循环中包含的所有下标都不会是1,后续的计算不会受到影响。
2.错误。注意到在i%k==0时才会执行该语句,所以f[i]f[i]必然包含c[i×k]=c[i]+1c[i×k]=c[i]+1
3.错误。ff数组存储约数个数,gg数组存储约数和。均不为单调递增。可以举反例如g[8]=1+2+4+8,g[9]=1+3+9g[8]=1+2+4+8,g[9]=1+3+9.
4.线性筛时间复杂度为线性,选A
5.ff数组存约数个数,约数个数为2即只包含1和本身,即为质数,1至100有25个质数
6.ff存约数个数,gg存约数和。1000=(23)×(53)1000=(23)×(53).套公式计算即可
解析:ABBACC
19.填空题(15分)
(Josephus 问题)有 nn 个人围成一个圈,依次标号 0 至 n−1n−1。从 0 号开始,依次 0, 1, 0, 1, ... 交替报数,报到 1 的人会离开,直至圈中只剩下一个人。求最后剩下人的编号。
试补全模拟程序。
#include <stdio.h>
const int MAXN = 1000000;
int F[MAXN];
int main(){
int n;
scanf("%d", &n);
int i = 0, p = 0, c = 0;
while( ①){
if (F[i] == 0){
if ( ② ){
F[i] = 1;
③;
}
④;
}
⑤;
}
int ans = -1;
for (int i = 0; i < n; i++)
if (F[i] == 0)
ans = i;
printf("%d\n", ans);
return 0;
}
①处应填()
②处应填()
③处应填()
④处应填()
⑤处应填()
1.
A.i < n
B.c < n
C.i < n - 1
D.c < n - 1
2.
A.i % 2 == 0
B.i % 2 == 1
C.p
D.!p
3.
A.i++
B.i = (i+1) % n
C.c++
D.p ^= 1
4.
A.i++
B.i = (i+1) % n
C.c++
D.p ^= 1
5.
A.i++
B.i = (i+1) % n
C.c++
D.p ^= 1
解析:
变量与数组作用:
数组FF:由第22,23行发现FF与答案输出有关,当F[i]F[i]为0时输出答案,因此可知FF为标记是否出圈的数组。F[i]=0F[i]=0代表未离开,为1代表已离开
变量cc:观察有cc的选项。发现特殊的,第一空中可能填入cc,而第一空为whilewhile的边界条件。由题意可知循环结束条件为出圈人数达到n−1n−1,联系选项可得cc代表出圈人数。
变量ii:根据日常使用习惯结合题目选项合理考虑,可以猜测i为当前进行判定的位置,实际上确实如此
变量pp:剩余一个变量为pp不知道作用。阅读题面发现“交替出圈”还未实现,且pp初始化为0。结合第二空的选项以及第二空决定F[i]F[i]是否等于1(即是否出圈)来看,可以得知pp用于判断当前人是否应当出圈。pp为0则不出, pp为1则出圈。
1.cc代表出圈人数,由题面可知出圈n−1n−1个则循环结束
2.由上推导可得,此处用于决定是否出圈,则与pp有关。若pp为1则出圈
3.有一人出圈,出圈人数cc增加
4.实现pp的01交替,0变1,1变0,使用异或1实现
至此只剩一个操作也就是移动当前考虑的位置,注意到人围成一个环,因此需要进行取模。
答案:DCCDB
20.填空题(15分)
(矩形计数)平面上有nn个关键点,求有多少个四条边都和xx轴或者yy轴平行的矩形,满足四个顶点都是关键点。给出的关键点可能有重复,但完全重合的矩形只计一次。
试补全枚举算法。
1 #include <stdio.h>
2
3 struct point {
4 int x, y, id;
5 };
6
7 int equals(struct point a, struct point b){
8 return a.x == b.x && a.y == b.y;
9 }
10
11 int cmp(struct point a, struct point b){
12 return ①;
13 }
14
15 void sort(struct point A[], int n){
16 for (int i = 0; i < n; i++)
17 for (int j = 1; j < n; j++)
18 if (cmp(A[j], A[j - 1])){
19 struct point t = A[j];
20 A[j] = A[j - 1];
21 A[j - 1] = t;
22 }
23 }
24
25 int unique(struct point A[], int n){
26 int t = 0;
27 for (int i = 0; i < n; i++)
28 if (②)
29 A[t++] = A[i];
30 return t;
31 }
32
33 int binary_search(struct point A[], int n, int x, int y){
34 struct point p;
35 p.x = x;
36 p.y = y;
37 p.id = n;
38 int a = 0, b = n - 1;
39 while(a < b){
40 int mid = ③;
41 if (④)
42 a = mid + 1;
43 else
44 b = mid;
45 }
46 return equals(A[a], p);
47 }
48
49 #define MAXN 1000
50 struct point A[MAXN];
51
52 int main(){
53 int n;
54 scanf("%d", &n);
55 for (int i = 0; i < n; i++){
56 scanf("%d %d", &A[i].x, &A[i].y);
57 A[i].id = i;
58 }
59 sort(A, n);
60 n = unique(A, n);
61 int ans = 0;
62 for (int i = 0; i < n; i++)
63 for (int j = 0; j < n; j++)
64 if ( ⑤ && binary_search(A, n, A[i].x, A[j].y) && binary_search(A, n, A[j].x, A[i].y)){
65 ans++;
66 }
67 printf("%d\n", ans);
68 return 0;
69 }
①处应填()
②处应填()
③处应填()
④处应填()
⑤处应填()
1.
A.a.x != b.x ? a.x < b.x : a.id < b.id
B.a.x != b.x ? a.x < b.x : a.y < b.y
C.equals(a,b) ? a.id < b.id : a.x < b.x
D.equals(a,b) ? a.id < b.id : (a.x != b.x ? a.x < b.x : a.y < b.y)
2.
A.i == 0 || cmp(A[i], A[i - 1])
B.t == 0 || equals(A[i], A[t - 1])
C.i == 0 || !cmp(A[i], A[i - 1])
D.t == 0 || !equals(A[i], A[t - 1])
3.
A.b - (b - a) / 2 + 1
B.(a + b + 1) >> 1
C.(a + b) >> 1
D.a + (b - a + 1) / 2
4.
A.!cmp(A[mid], p)
B.cmp(A[mid], p)
C.cmp(p, A[mid])
D.!cmp(p, A[mid])
5.
A.A[i].x == A[j].x
B.A[i].id < A[j].id
C.A[i].x == A[j].x && A[i].id < A[j].id
D.A[i].x < A[j].x && A[i].y < A[j].y
解析:比较清晰的一道题,主要在于函数名都给的比较清晰,大大降低了解读难度。根据binary_searchbinary_search函数名我们可以得知这题使用二分。sortsort一般是用于排序,显然这道题中需要排序的就是点的坐标,同时用于满足二分的单调性。uniqueunique由函数名就知道很可能是用于去重,观察主函数中正好在sortsort排序之后,同时题面说明完全重合矩阵只计一次,确定了就是去重的作用。接下来主函数中两层循环枚举了两个点进行两个二分。显然满足题目条件的四边形可以由对角的两个点得知整个图形另外两个点的位置。如:若枚举两点为左下角(x1x1,y1y1)与右上角(x2x2,y2y2),那么我们就能求得左上角为(x1x1,y2y2),右下角为(x2x2,y1y1)。至此我们就可以推出二分的意义实际上是在枚举两个点后用于二分查找另外两个点是否存在于所给点集中。
梳理一下流程就是这样:
1.输入点集中各点的坐标
2.坐标排序,使得数据满足单调性
3.坐标去重,相同关键点只计一次
4.枚举左下角与右上角点的坐标,二分查找答案
解题流程就很清晰了。
答案解析:
1.cmpcmp显然是排序的规则。我们排的是点的坐标,因此与idid无关。从右下往左上排即可:xx不同时按xx从小到大排序,xx相同时按yy从小到大排序,这也是二维坐标系中最常见的排序方式
2.考察去重写法。tt记录不同的点的个数。从小到大,发现有不同的点就存储(或者为第一个点),依然用AA存。返回不同的点的个数。
3.二分基本代码。位运算每右移1位表示除一个2,每左移一位表示乘一个2.注意此处为二分查找左边界,不用+1.
4.左边界右移,是A[mid]A[mid]小于pp的情况。
5.发现枚举时并没有考虑ii和jj相等或两点在同一条直线的情况,因此此处就用于保证枚举的两点分别为左下角与右上角。
答案:BDCBD
以上就是所有内容啦!
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)
