问题描述
文中所有图片引用自原文 Tackling the Qubit Mapping Problem for NISQ-Era Quantum Devices
问题描述
文章介绍了将编写的量子电路映射为运行在真实设备上的方法。
在真实设备上,一个量子位只能与物理上相连的量子位进行运算。单量子门并不受这一限制的影响,而对于多量子门,如CNOT门,参与运算的量子位必须直接相连。由于任意多量子门都可拆分为多个单量子门和CNOT门的运算,因此我们只需研究如何处理CNOT门。
解决方案
符号约定
| 符号 | 定义 |
|---|---|
| n n n | 逻辑量子位数量 |
| { q i } i = 1 n \{q_i\}_{i=1}^{n} {qi}i=1n | 逻辑量子位 |
| g g g | 电路量子门数量 |
| d d d | 电路深度 |
| N N N | 物理量子位数量 |
| { Q i } i = 1 n \{Q_i\}_{i=1}^n {Qi}i=1n | 物理量子位 |
| G ( V , E ) G(V,E) G(V,E) | 物理设备芯片抽象得到的图结构 |
| D ( Q i , Q j ) D(Q_i,Q_j) D(Qi,Qj) | Q i Q_i Qi 与 Q j Q_j Qj 间距离 |
| π ( q i ) \pi(q_i) π(qi) | q i q_i qi 当前对应的物理量子位 |
| π − 1 ( Q i ) \pi^{-1}(Q_i) π−1(Qi) | Q i Q_i Qi 当前对应的逻辑量子位 |
| F \mathbb F F | Front Layer |
| E \mathbb E E | Extended Set |
简要思路
文中给出的方法是:对于逻辑上参与CNOT门的两个量子位 q i q_i qi 和 q j q_j qj,若两者在物理上的映射并不相邻,则通过一系列SWAP操作,使得两者在物理上的映射相邻,即在电路中额外引入若干SWAP操作,使得电路在真实设备上可运行。

文中使用一个DAG表示CNOT门之间的依赖关系,用拓扑排序的方式依次处理各个CNOT门。图中的结点表示一个CNOT门,边表示后继结点表示的CNOT门需要等待的量子位。
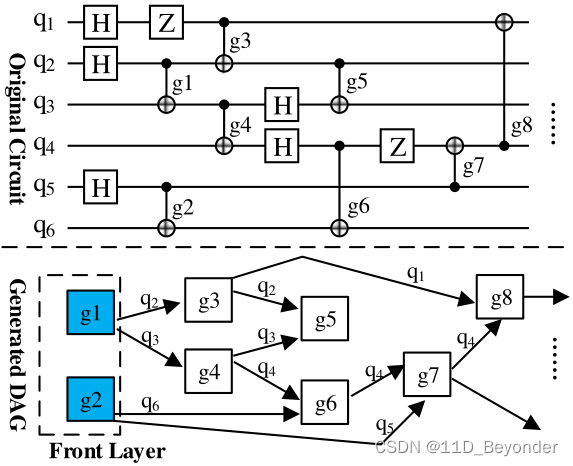
拓扑排序的队列为 F \mathbb F F,文中称为 Front Layer。在拓扑排序的循环中,从 F \mathbb F F 中挑出可直接在物理设备上执行的CNOT门,放入集合 S g \mathbb S_g Sg;若 S g ≠ ∅ \mathbb S_g\neq\varnothing Sg=∅,则执 S g \mathbb S_g Sg 中的CNOT门,并更新 F \mathbb F F;若 S g = ∅ \mathbb S_g=\varnothing Sg=∅,则枚举所有可行的SWAP操作,执行评估函数值最优秀的SWAP操作,更新 π \pi π 和 π − 1 \pi^{-1} π−1。
预处理
预处理阶段主要干四件事情:
- 计算距离矩阵 D D D,可简单认为芯片上的边都是双向的,边权都为 1 1 1,可用Floyd或者Johnson算法求全源最短路;
- 根据逻辑电路生成DAG;
- 初始化 F \mathbb F F;
- 初始化 π \pi π 和 π − 1 \pi^{-1} π−1。
SWAP操作枚举方法
显然,只有使得 F F F 中的CNOT门可执行的SWAP操作才能使得拓扑排序不断进行下去,因此枚举SWAP操作时仅考虑 F \mathbb F F 中的门电路。
枚举 F F F 中的CNOT门,设参与某一CNOT门运算的两比特为 q i q_i qi 和 q j q_j qj,取其中一个比特的物理映射 Q x = π ( q i ) Q_x=\pi(q_i) Qx=π(qi),找到 Q x Q_x Qx 的邻接点集合 Q x ⋅ \mathbb Q_{x\cdot} Qx⋅, q i q_i qi 可与 π − 1 ( Q x ⋅ ) \pi^{-1}\left(\mathbb Q_{x\cdot}\right) π−1(Qx⋅) 进行SWAP操作。
评估函数 H H H
一个SWAP操作使用评估函数 H H H 计算得分, H H H 越小则SWAP操作越优秀。
假设执行SWAP之后的映射为
π
t
\pi_t
πt,评价函数可表示为
H
(
SWAP
(
q
x
,
q
y
)
)
=
max
(
decay
(
q
x
)
,
decay
(
q
y
)
)
⋅
1
∣
F
∣
∑
CNOT
(
q
i
,
q
j
)
∈
F
D
(
π
t
(
q
i
)
,
π
t
(
q
j
)
)
+
W
⋅
1
∣
E
∣
∑
CNOT
(
q
i
,
q
j
)
∈
E
D
(
π
t
(
q
i
)
,
π
t
(
q
j
)
)
H(\text{SWAP}(q_x,q_y))=\max(\text{decay}(q_x),\text{decay}(q_y))\cdot\frac{1}{|\mathbb F|}\sum\limits_{\text{CNOT}(q_i,q_j)\in\mathbb F}D(\pi_t(q_i),\pi_t(q_j))+W\cdot\frac{1}{|\mathbb{E}|}\sum\limits_{\text{CNOT}(q_i,q_j)\in\mathbb E}D(\pi_t(q_i),\pi_t(q_j))
H(SWAP(qx,qy))=max(decay(qx),decay(qy))⋅∣F∣1CNOT(qi,qj)∈F∑D(πt(qi),πt(qj))+W⋅∣E∣1CNOT(qi,qj)∈E∑D(πt(qi),πt(qj))
总体来看,
H
H
H 体现了执行SWAP操作后参与运算的量子位之间的靠近程度。
decay
(
q
i
)
\text{decay}(q_i)
decay(qi) 初始化为
1
1
1,当
q
i
q_i
qi 参与一次SWAP操作,则
decay
(
q
i
)
\text{decay}(q_i)
decay(qi) 增加
δ
\delta
δ,这使得算法趋向于选择多个量子位运算不冲突的SWAP操作,使得多个SWAP操作可以并行执行。
E
\mathbb E
E 是 Extended Set,即
F
\mathbb F
F 的一部分后继;为了使得算法有较好的预见性,因此将
E
\mathbb E
E 中的量子门也纳入评估。
初始映射 π \pi π 优化
π \pi π 的初始化对最终结果有很大影响,因此需要优秀的 π \pi π 值。
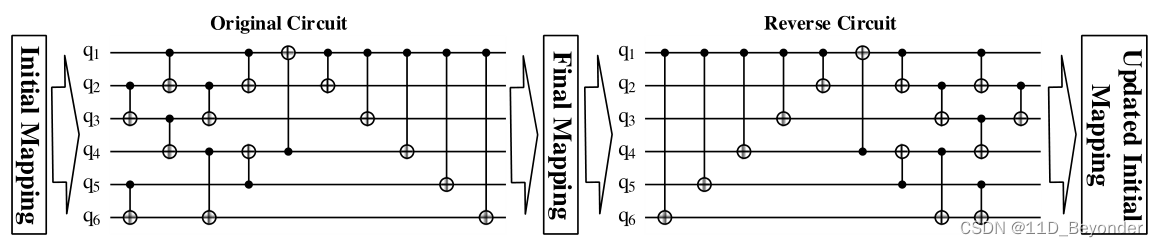
文中运用了一个 trick:量子电路的正向执行与反向执行是等价的,因此首先随机初始化 π = π s \pi=\pi_s π=πs,用正向电路执行一遍上述算法得到 π = π f \pi=\pi_f π=πf, π f \pi_f πf 对于反向电路来说是一个优秀的初始化映射;再用 π f \pi_f πf 作为初始化映射,用反向电路运行上述算法得到 π = π u \pi=\pi_u π=πu 得到优秀的正向电路初始化映射。
思考
- 注意到DAG上的结点的出度和入度至多为2,这可能是可以进一步改进算法的地方。
- 文中是基于IBM的量子芯片设计的算法,对于一些非对称的芯片(边是单向的),需要考虑新的优化算法。
解决方法
暂无找到可以解决该程序问题的有效方法,小编努力寻找整理中!
如果你已经找到好的解决方法,欢迎将解决方案带上本链接一起发送给小编。
小编邮箱:dio#foxmail.com (将#修改为@)
