题面
分析
通过观察我们可以发现,这是一道 2-SAT 问题,因为我们有 q 个两两相关的限制条件,于是我们可以考虑建图来跑 (于是建图这一步这么快就出来了)。
因为我们的限制条件是按位或,因此我们可知在二进制下各个位是相互独立的,于是我们可以分开讨论,并且我们发现我们只需要对每个位上都求出字典序最小的情况,我们就得到了整个的字典序最小。
建图
我们考虑怎么建图:由于是 2-SAT 问题,假定每个数的当前位为点,那么每一对限制条件就是一条无向边(因为他们的限制是相互的)。
我们分 3 中情况讨论:
-
已经确定:通过观察我们可以发现,如果给定的 a = = b a == b a==b 那么我们就已经可以确定 a n s [ a ] = x ans[a] = x ans[a]=x(ans即为最终输出结果),注意 a 是下标(注意看题)。那么我们在分位讨论的时候只需要给他所对应的点上一个特殊标记,告诉程序我们将不再动他即可(比如为 1 就给他赋值为 2,为 0 就直接赋值为 0,因为我们后面将只处理权值为 1 的节点)。
-
限制为0:在一对限制条件中,我们不难发现,如果 x 在这一位是 0,那么我们就可以断定 ans[a] 和 ans[b] 的这一位都是 0(由按位或的性质)。那么我们可以在建图的时候就直接让这两个点的权值赋为 0,然后再也不动他即可。(由于要求字典序最小,于是已经被赋为 0 的位我们将不会再动)。
-
限制为1:再考虑 x 这一位是 1 的情况,我们先假定除了以上两种特殊处理的点以外的点的权值都为 1,然后将每一对这样的限制连上边(上面两种已经确定的情况可以不建)。我们从节点 1 开始(也就是对应原序列的第一个数)遍历所有他所连向的点,如果其中由任何一个权值为 0(前面赋的初值,或者后面处理的),那么我们可以确定这个点只能为 1。否则我们就把它赋为 0(为了保证字典序最小)。最后所有点更新完之后更新答案即可。(注意:已经赋值为 0 或 2 的点我们将不会再动,因为他们已经确定了)。
当所有位都跑完我们就得到了最终答案。
注意:如果某个点被孤立了(没有连边),那么他直接为 0 是最优的。
eg. 我们以原题中的样例一为例:
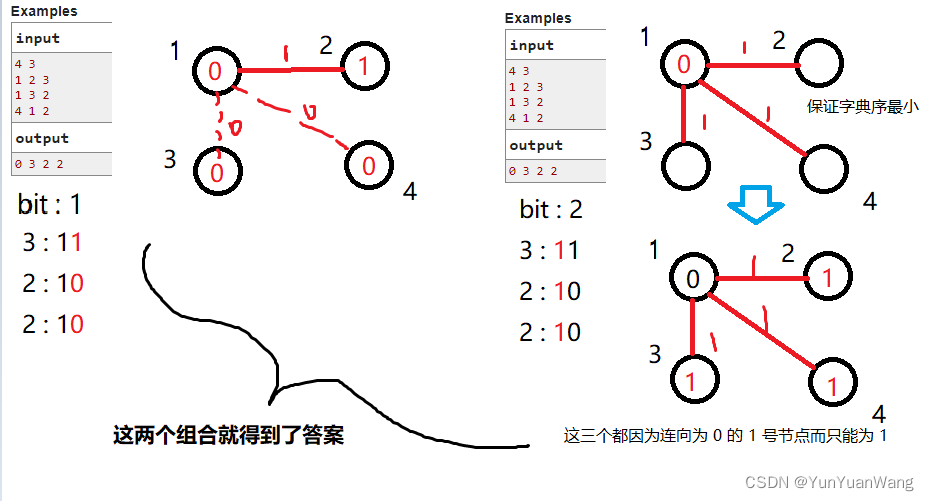
上图中边上的权值表示限制中的 x 这一位是什么。
代码实现
//省略快读和头文件
#define Ql Qualifications//为了简写用
int T;
struct Edge {
int hd[MAXN];
int nxt[MAXN << 2], to[MAXN << 2];
int tot = 0;
void Add(int x, int y) {
nxt[++tot] = hd[x];
hd[x] = tot;
to[tot] = y;
}
}e;
int n, q;
int ans[MAXN];
struct Qualifications {
int a, b, x;
}p[MAXN << 1];
int dig[MAXN];
void Solve(int pos)
{
memset(e.hd, 0, sizeof(e.hd));//记得清空
e.tot = 0;
for(int i = 1; i <= n; i++)
dig[i] = 1;
for(int i = 1; i <= q; i++) {
if(p[i].a == p[i].b) {
if((p[i].x >> pos) & 1)
dig[p[i].a] = 2;//表示为 1,且固定不再修改
else
dig[p[i].a] = 0;//如果是 0,直接为 0 即可,因为我们本来就不动他
continue;
}
if((p[i].x >> pos) & 1) {//如果是 1 就说明需要连边来判断如何填
e.Add(p[i].a, p[i].b);
e.Add(p[i].b, p[i].a);
}else {
dig[p[i].a] = dig[p[i].b] = 0;//如果是 0 那么直接赋值为 0 即可,由按位或的性质
}
}
for(int x = 1; x <= n; x++) {
if(dig[x] == 0 || dig[x] == 2)
continue;//这两种都是已经固定的
bool flag = true;//表示可以更改为 0
for(int i = e.hd[x]; i; i = e.nxt[i]) {
int y = e.to[i];
if(dig[y] == 0) {//只要连向的点有一个是 0 就说明他一定是 1
flag = false;
break;
}
}
if(flag || !e.hd[x])//否则将他赋值为 0 一定更优(字典序最小)
dig[x] = 0;//同样如果这个点是独点,那么他一定为 0 更优
}
for(int i = 1; i <= n; i++)
ans[i] |= (dig[i] > 0) * (1 << pos);
}
int main()
{
n = inpt(), q = inpt();
for(int i = 1; i <= q; i++) {
int a = inpt(), b = inpt(), x = inpt();
if(a == b)//表示这一个已经确定了
ans[a] = x;
p[i] = Ql{a, b, x};//看不懂就看第1行和第19行
}
for(int i = 0; i < 31; i++)//分位做
Solve(i);
for(int i = 1; i <= n; i++)
printf("%d ", ans[i]);
return 0;
}






