JavaScript —— 算法思想之递归
《工欲善其事,必先利其器》

一、算法思想之递归
什么是递归?
递归,就是我们在求某个具有规律性的数据过程中,反复执行求值的这个过程。而这种反复执行的套路,我们一般把其称之为规则复现。
引用数学界非常著名的一个数学问题来证实我们的猜想 —— 《斐波那契数列》。
问题如下:
解法1:不使用递归
// 可以把这个数组看成斐波那契数列,第0项和第1项的值永远为1,否则将永无止境。
const fibArr = [1, 1];
// 开始计算第十项的数列值
while(fibArr.length <= 9) {
fibArr.push(fibArr[fibArr.length - 1] + fibArr[fibArr.length - 2]);
}
alert(fibArr[9])
查看效果:

虽说这种方法可以求出这个值,但是它并没有使用到递归的方式,不契合我们今天本篇文章的重点。当然了,解决问题的方法很多,不一定需要使用到算法。上面的数组解决方式就是一个例子。而我们今天主要学习的是,递归的思想。
解法2:运用递归
// 封装一个递归函数,同时判断0和1的极限值
function fib(n) {
return n == 0 || n == 1 ? 1 : fib(n-1) + fib(n-2);
}
alert(fib(9));
查看效果:

看见了吗?我只用了3行代码,就能求出第十项的值。甚至于,这份新的代码看起来,比上面数组的方法,还要优雅得多。这就是非常典型的:递归函数。
但,其实,这种解法看似优雅,实则却是会耗费挺多资源的。例如:
fib(3) = fib(2) + fib(1);而fib(2) = fib(1) + fib(0)。其中,fib(1),会被计算两次。这就意味着,当 n = 10000 时,这个计算的代价是非常巨大的。因此,我们需要借助缓存的算法思想。
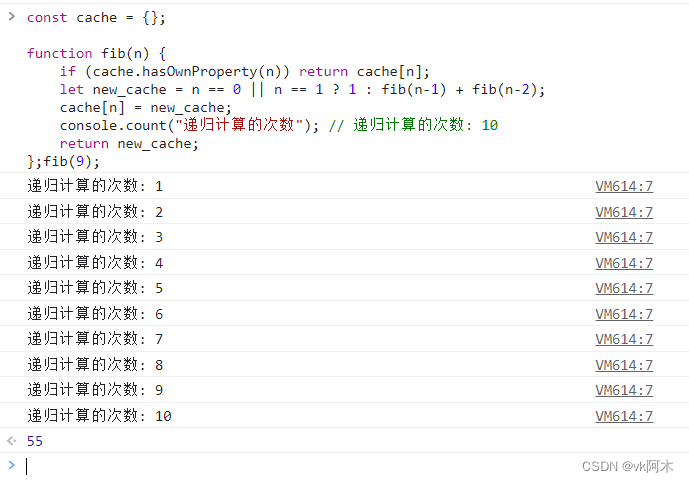
解法3:递归缓存优化
const cache = {};
function fib(n) {
if (cache.hasOwnProperty(n)) return cache[n];
let new_cache = n == 0 || n == 1 ? 1 : fib(n-1) + fib(n-2);
cache[n] = new_cache;
console.count("递归计算的次数"); // 递归计算的次数: 10
return new_cache;
}
同样,我们也是应用递归的思想。不同的是,与此同时我们加以利用缓存的思想,对取值进行判断。若命中缓存,直接返回结果,无需计算;反之就计算递归值。
相比解法2中数以万计的计算次数,解法3仅需要10次计算就可以获得数列值。可见合理的运用算法思想是可以为我们的编程效率带来巨大甚至是巨额的提升!!!
这时候,我相信有小年轻会提问了:
- 看你讲到这里,怎么感觉还倒退了??还没第一种方法好使啊!你个辣鸡!!!
那你要这么说的话,我只能给你来点有深度的题目给你解了。。。我们一起看看下面这道题:
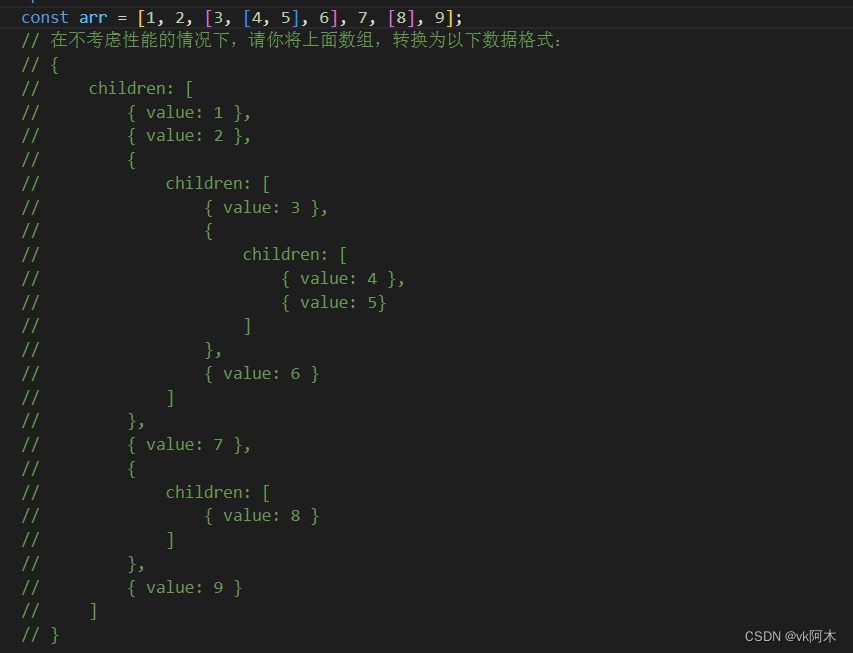
麻烦你,不要使用递归,实现一下???

解法1:使用递归
function arrayToTokens(arr) {
let token;
const resultArray = [];
for(let i = 0; i < arr.length; i++) {
token = arr[i];
if (!Array.isArray(token)) {
resultArray.push({ value: token });
} else {
resultArray.push({ children: arrayToTokens(token) });
}
}
return resultArray;
}
这里我们运用递归,也能够很轻松的解决这道题目。除此之外,我们还有另外一种解题思路,也是同样可以解决这个问题,而且基本上,差别不大。
二、算法思想之映射
我们在面对已知的数据结构时,如果需要对数据结构进行改写。例如上面第二个问题,我们知道数组的长度,那么我们可以尝试运用映射的思想去解决这个问题:
解法2:使用映射思想
function arrayToTokens(items) {
if (!Array.isArray(items)) {
return { value: items };
}
return { children: items.map(_item => arrayToTokens(_item)) };
}
解法1第一次调用函数的时候,就开始使用递归函数了;而解法2第一次调用函数的时候,则是先判断,把递归交给下一次函数的调用。解法2比解法1只多了一次调用。
但这只是建立在我们知道,需要处理的数据源的数据结构的基础上。如果我们不清楚数据源的长度或是结构,那么我们是一定要使用循环去一个个排除不对等的情况,然后再使用递归,改写数据结构。
三、总结
-
指针思想 - 在计数或比较大小的情况使用得多,不仅可以处理字符串,有的时候也可以处理对象。被指到的对象如果符合某个条件,就需要做一些操作。核心就是:遍历+判断+一次性过,效率高; -
递归思想 - 请记住一个词:规则复现。不管是字符串还是对象,只要符合规则符现的情况,就可以考虑使用递归。当然,使用递归的过程种,注意要合理运用缓存和映射思想,有时可以提高递归的效率!!
最后,感谢你的阅读。






