pythonA算法找出数据集中满足条件的关联规则

目录

1.数据集

2.Apriori算法原理

3.实现步骤

3.1A算法函数

3.2获取频繁项集函数

3.3候选集函数

3.4扫描候选集函数

3.5主函数

4.运行结果

 5.全部代码

---

1.数据集

[[1, 2, 5], [2, 4], [2, 3], [1,2,4],[1,3],[2,3],[1,3],[1,2,3,5],[1,2,3]]

可自行定义为所需的数据集。

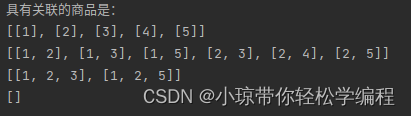
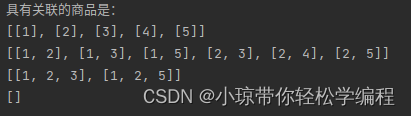
执行程序后，找到具有关联的商品，并且输出其对应的结果：

2.Apriori算法原理

Apriori算法是经典的挖掘频繁项集和关联规则的数据挖掘算法。Apriori算法使用一种称为逐层搜索的迭代方法，其中k项集用于探索（k+1）项集。为了提高频繁项集逐层产生的效率，Apriori算法使用频繁项集的先验性质来压缩搜索空间。先验性质为：

频繁项集的所有非空子集也一定是频繁的。非频繁项集的所有超集一定也是非频繁项集。

3.实现步骤

3.1A算法函数，其最小置信度为0.2

def A(dataset, min_support = 2):
    c1 = item (dataset)
    f1, sup_1 = get_f_i(dataset, c1, min_support)
    F = [f1]
    sup_data = sup_1
    K = 2
    while (len(F[K - 2]) > 1):
        ck = get_c(F[K - 2], K)
        fk, sup_k = get_f_i(dataset, ck, min_support)
        F.append(fk)
        sup_data.update(sup_k)
        K += 1
    return F, sup_data

使用item函数扫描候选集，再使用get_f_i函数获取频繁项集，通过一系列的获取候选集和频繁项集以此来实现A算法。

3.2获取频繁项集函数

def get_f_i(dataset, c, min_support): #获取频繁项集
    cut_branch = {}
    for x in c:
        for y in dataset:
            if set(x).issubset(set(y)):
                cut_branch[tuple(x)] = cut_branch.get(tuple(x), 0) + 1
    Fk = []
    sup_dataK = {}
    for i in cut_branch:
        if cut_branch[i] >= min_support:
            Fk.append( list(i))
            sup_dataK[i] = cut_branch[i]
    return Fk, sup_dataK

3.3候选集函数

def get_c(Fk, K):
    ck = []
    for i in range(len(Fk)):
        for j in range(i+1, len(Fk)):
            L1 = list(Fk[i])[:K-2]
            L2 = list(Fk[j])[:K-2]
            L1.sort()
            L2.sort()
            if L1 == L2:
                if K > 2:
                    new = list(set(Fk[i]) ^ set(Fk[j]))
                else:
                    new = set()
            for x in Fk:
                if set(new).issubset(set(x)) and list(set(Fk[i]) | set(Fk[j])) not in ck:
                    ck.append(list(set(Fk[i]) | set(Fk[j])))
    return ck

3.4扫描候选集函数

def item(dataset):
    c1 = []
    for x in dataset:
        for y in x:
            if [y] not in c1:
                c1.append( [y] )
    c1.sort()
    return c1

3.5主函数

if __name__ == '__main__':
    data = [[1, 2, 5], [2, 4], [2, 3], [1,2,4],[1,3],[2,3],[1,3],[1,2,3,5],[1,2,3]]
    K,Z= A(data,min_support = 2)   #最小支持度设置为2
    print("具有关联的商品是：")
    for i in range(len(K)):人工智能
        print(K[i])

4.运行结果，如下图所示：

 5.全部代码

def A(dataset, min_support = 2):
    c1 = item (dataset)
    f1, sup_1 = get_f_i(dataset, c1, min_support)
    F = [f1]
    sup_data = sup_1
    K = 2
    while (len(F[K - 2]) > 1):
        ck = get_c(F[K - 2], K)
        fk, sup_k = get_f_i(dataset, ck, min_support)
        F.append(fk)
        sup_data.update(sup_k)
        K += 1
    return F, sup_data
def get_f_i(dataset, c, min_support): #获取频繁项集
    cut_branch = {}
    for x in c:
        for y in dataset:
            if set(x).issubset(set(y)):
                cut_branch[tuple(x)] = cut_branch.get(tuple(x), 0) + 1
    Fk = []
    sup_dataK = {}
    for i in cut_branch:
        if cut_branch[i] >= min_support:
            Fk.append( list(i))
            sup_dataK[i] = cut_branch[i]
    return Fk, sup_dataK
def get_c(Fk, K):
    ck = []
    for i in range(len(Fk)):
        for j in range(i+1, len(Fk)):
            L1 = list(Fk[i])[:K-2]
            L2 = list(Fk[j])[:K-2]
            L1.sort()
            L2.sort()
            if L1 == L2:
                if K > 2:
                    new = list(set(Fk[i]) ^ set(Fk[j]))
                else:
                    new = set()
            for x in Fk:
                if set(new).issubset(set(x)) and list(set(Fk[i]) | set(Fk[j])) not in ck:
                    ck.append(list(set(Fk[i]) | set(Fk[j])))
    return ck
def item(dataset):
    c1 = []
    for x in dataset:
        for y in x:
            if [y] not in c1:
                c1.append( [y] )
    c1.sort()
    return c1
if __name__ == '__main__':
    data = [[1, 2, 5], [2, 4], [2, 3], [1,2,4],[1,3],[2,3],[1,3],[1,2,3,5],[1,2,3]]
    K,Z= A(data,min_support = 2)   #最小支持度设置为2
    print("具有关联的商品是：")
    for i in range(len(K)):
        print(K[i])