【题目描述】
罗老师被邀请参加一个舞会,是在城市n,而罗老师当前所处的城市为1,附近还有很多城市2~n-1,有些城市之间没有直接相连的路,有些城市之间有直接相连的路,这些路都是双向的,当然也可能有多条。
现在给出直接相邻城市的路长度,罗老师想知道从城市1到城市n,最短多少距离。
【输入】
输入n, m,表示n个城市和m条路;
接下来m行,每行a b c, 表示城市a与城市b有长度为c的路。
【输出】
输出1到n的最短路。如果1到达不了n,就输出-1。
【输入样例】
5 5
1 2 20
2 3 30
3 4 20
4 5 20
1 5 100
【输出样例】
90
【提示】
【数据规模和约定】
1≤n≤2000
1≤m≤10000
0≤c≤10000
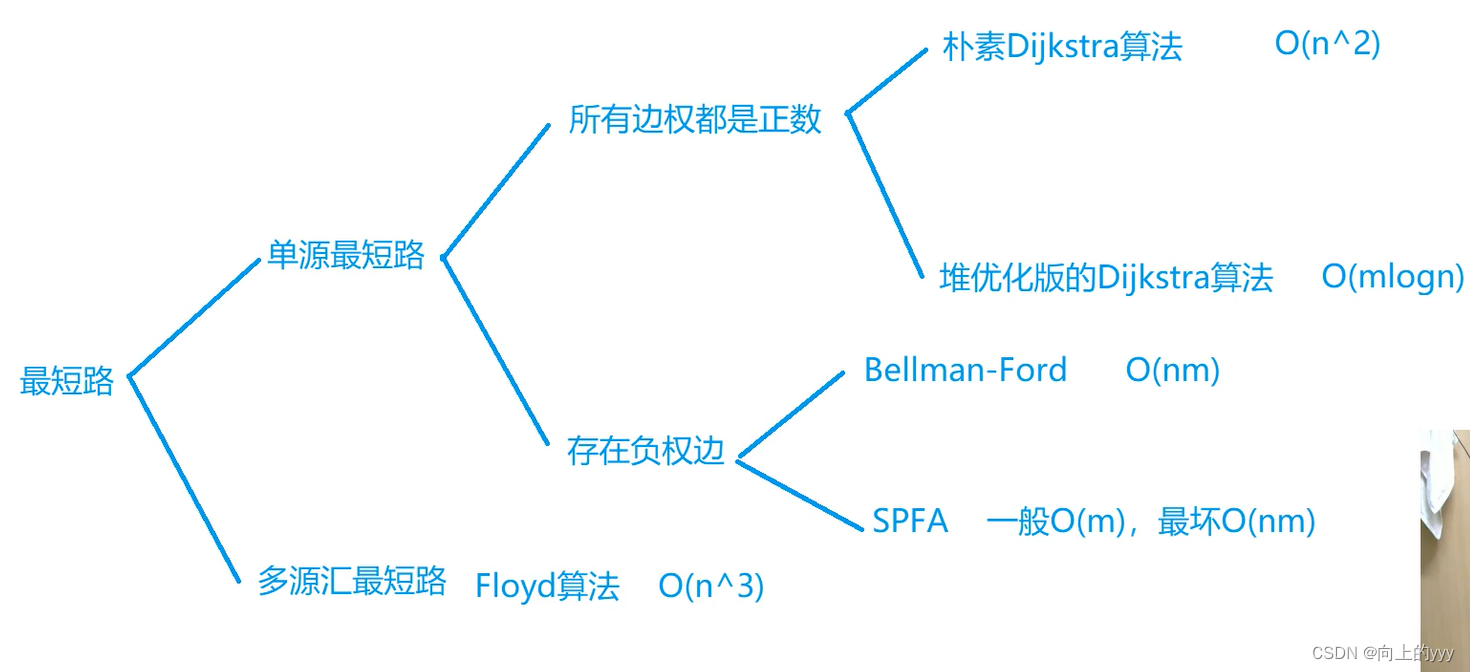
分析
- 根据n的范围可知此题用邻接矩阵存储图即可,以及O(n^2)的时间复杂度也是够用的,所以采用了朴素的Dijkstra算法,注意输入可能有重复边,我们要选最小的边;
- 算法思想就是:
- 先初始化起点到所有点的距离为0x3f3f3f3f,再把起始点的dist设为1;
- 然后就是n次迭代过程
- 先在还未确定最短路的点中,寻找距离最小的点(遍历这n个点,然后 !st[j] && (t == -1 || dist[t] > dist[j]) 这个条件,去选出n个点中,未被确定最短路的以及起点到达某点距离最短的点);将t点标记已确定最短路(st[t] = 1;)
- 然后找到这个t点(未确定最短路的点中,起点到该点距离最小的点),然后用t点更新这n个点的距离(dist[j] = min(dist[j], dist[t] + g[t][j]);),也就是看看有没有以t当做中间点,然后加上t到j这个点的距离(dist[t]+g[t][j]),是否比当前的距离dist[j]小;
- 参考acwing的模板:常用代码模板3——搜索与图论,以及最短路算法的总结;
#include <bits/stdc++.h>
using namespace std;
const int N = 2010, INF = 0x3f3f3f3f;
int g[N][N];// 存储每条边
int dist[N];// 存储1号点到每个点的最短距离
int st[N];// 存储每个点的最短路是否已经确定
int n, m;
int dijkstra() {
memset(dist, INF, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n; ++i) {
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; ++j) {
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
st[t] = 1;
// 用t更新其他点的距离
for (int j = 1; j <= n; ++j) {
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
}
if (dist[n] == INF)
return -1;
else
return dist[n];
}
int main() {
cin.tie(0);
cin >> n >> m;
memset(g, INF, sizeof g);
for (int i = 0; i < m; ++i) {
int a, b, c;
cin >> a >> b >> c;
//多条重复路
g[a][b] = min(g[a][b], c);
g[b][a] = g[a][b];
}
cout << dijkstra();
return 0;
}






