大纲
1.流网络&最大流
流网络简介
流网络G(V, E)是一个有向图,图中每条边(u, v)∈E都有一个非负权值c(u, v) ,称为边的容量。并
且,如果边集E包含一条边(u, v),则图中不存在反方向的边(v, u)。如果(u, v)∉ E,则c(u, v) = 0。
在流网络的所有节点中,有两个特殊节点:源点S和汇点T。
流网络示例:
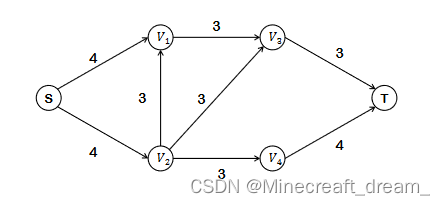
设G(V, E)是一个流网络,其容量函数为c,设S为网络的源点,T为网络的汇点。G中的流是一个实数函数f(u, v) (u∈V && v属于V)且满足以下性质:
① 容量限制:对于任意节点u, v∈V,要求:0 ≤ f(u, v) ≤ c(u, v)。
② 流量守恒:对于任意节点u∈V - {S,
T},要求:所有x∈Vf(x, u) = 所有y∈Vf(y, u)
③ 斜对称:f(u, v) = - f(v, u)
实例
例如下图的网络流量为5(流量/容量)。
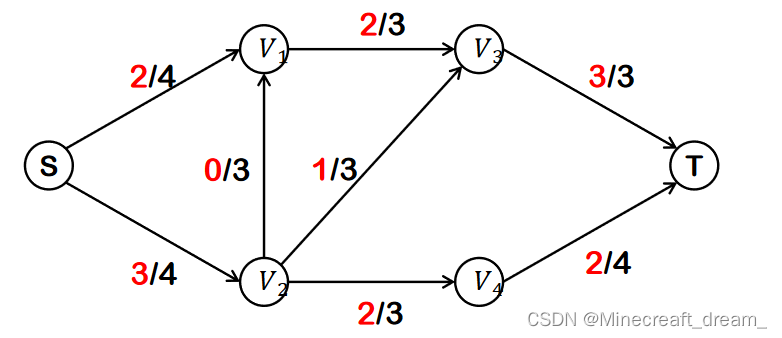
对于一个给定的网络,合法的流函数f有很多,其中使得整个网络的流量最大的流函数被称为网络的最大流,此时的流量被称为网络的最大流量。
例如:下图的流网络的最大流量为6(流量/容量)。
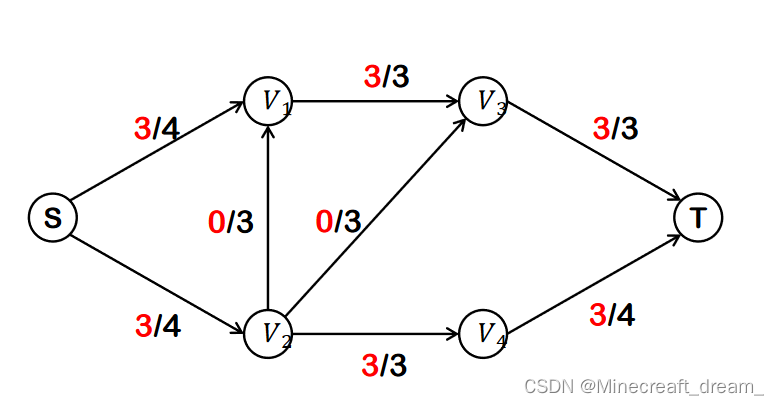
概念:
残留网络(残量网络):任意时刻,网络中所有节点以及剩余容量大于0的边构成的子图称为残留网络。
初始化:基于原始网络建立残存网络,初始化时残留网络和原网络一致。
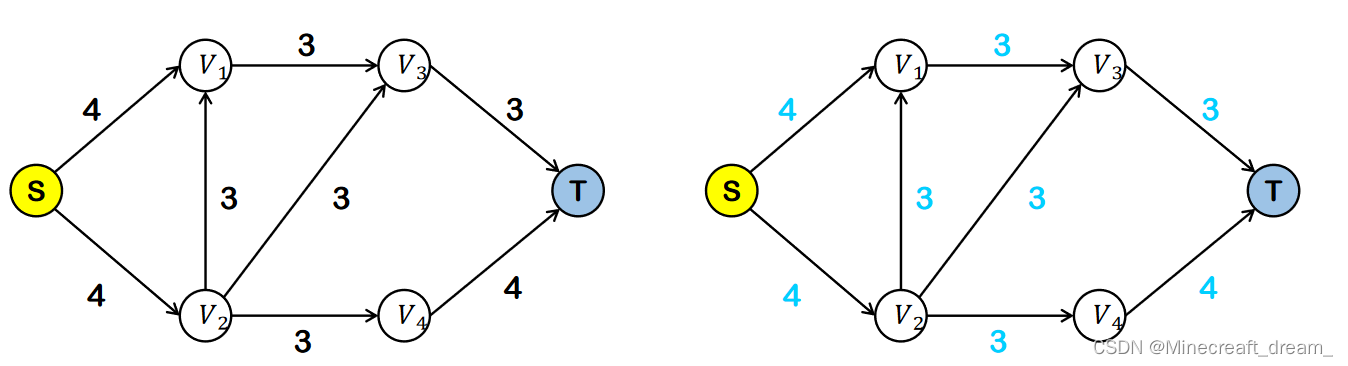
暴力求解最大流
第1步:从残存网络中找出一条从起点S到终点T的简单路径。
第2步:基于路径中容量最小的边,更新残留网络。
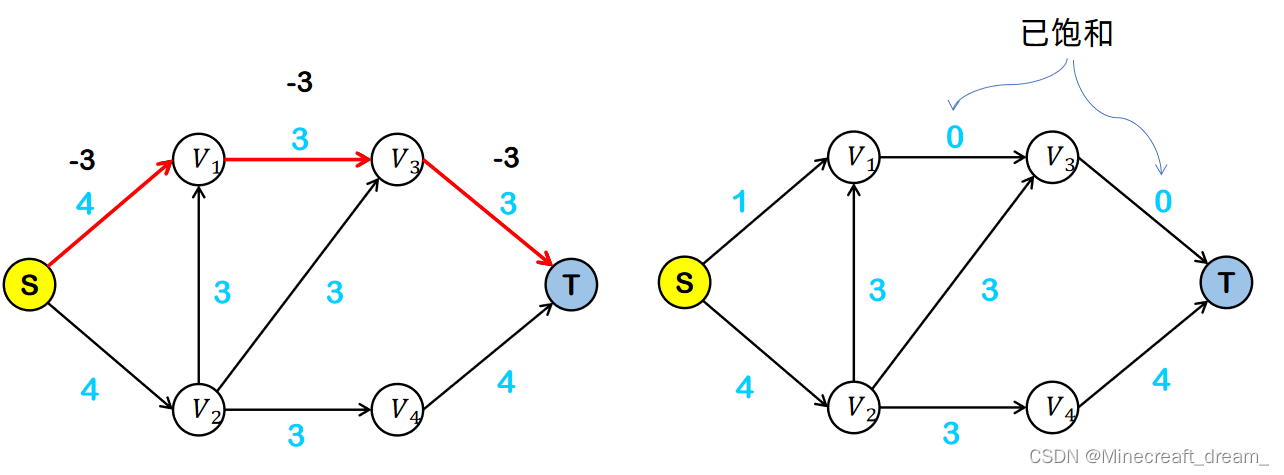
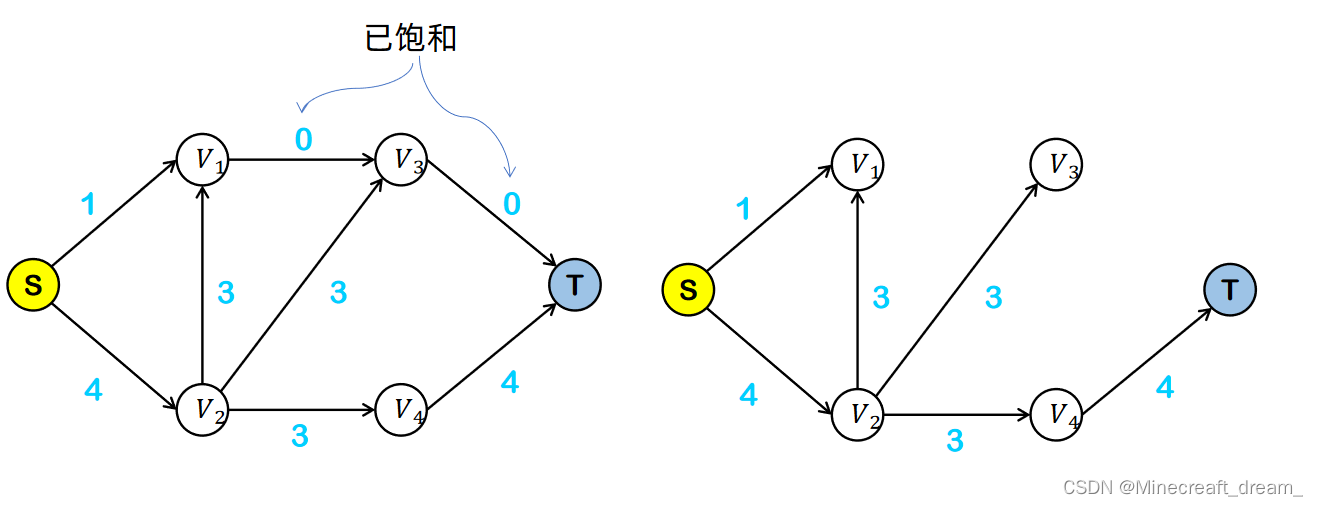
流量 = 容量 - 空闲量
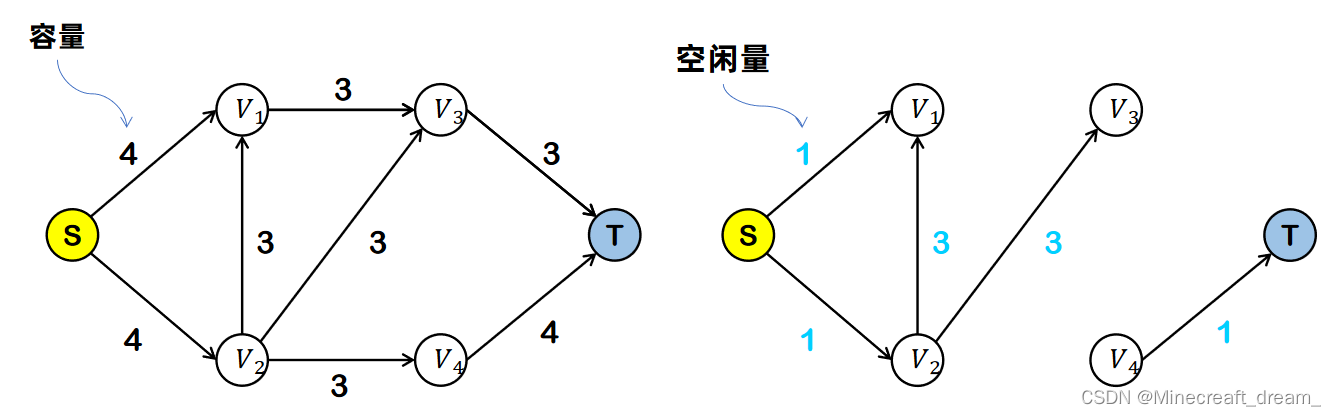
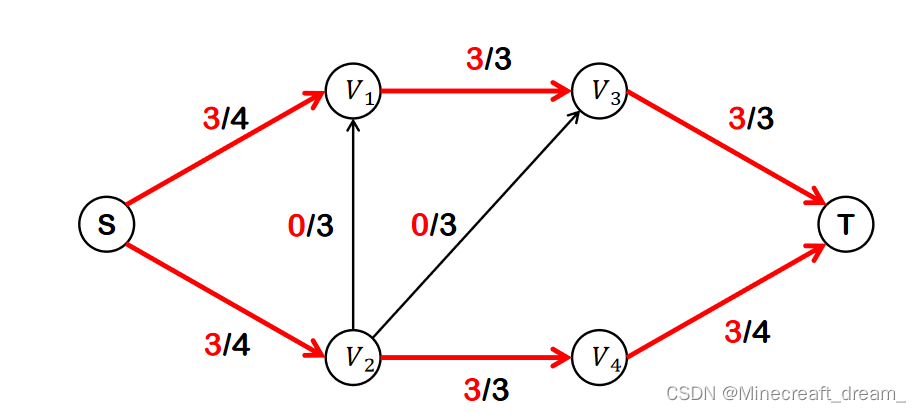
算法问题:上面描述的简单算法不能确保一定可以找到最大流。
简单算法计算出的流为阻塞流,最大流也是阻塞流的一种。
2.Edmonds-Karp算法求解
(1).ford-fulkerson算法
简单算法不会反悔,一旦被选中就不会再改变,ford-fulkerson是在简单算法上的一种改进算法,可以确保找到最大流。
初始化:基于原始网络建立残留网络,初始化时残留网络和原网络一致。
第1步:从残存网络中找出一条从起点S到终点T的简单路径。
第2步:基于路径中容量最小的边,更新残留网络。
第3步:从残留网络中删除已饱和的边。
第4步:添加一条反向路径,路径中边的容量 = 原路径的流量。
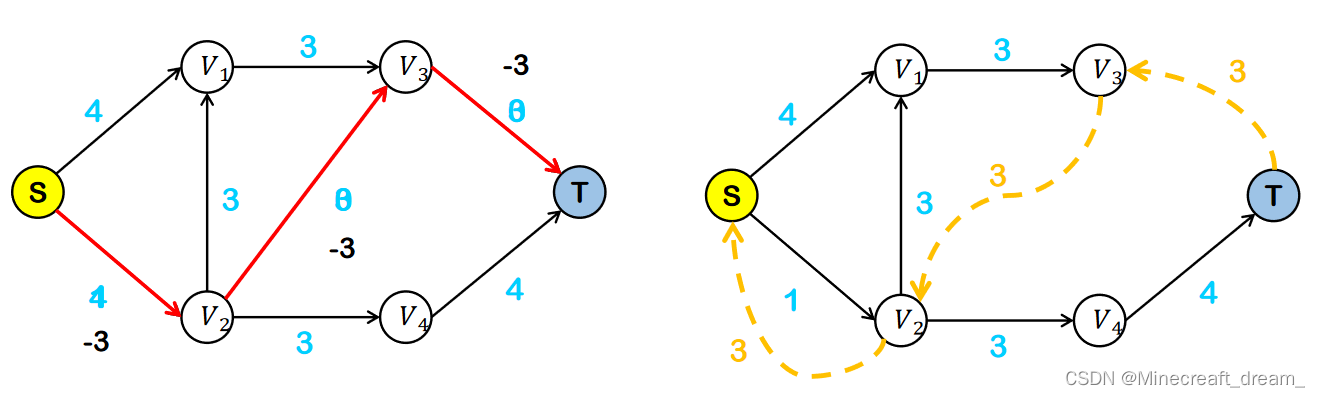
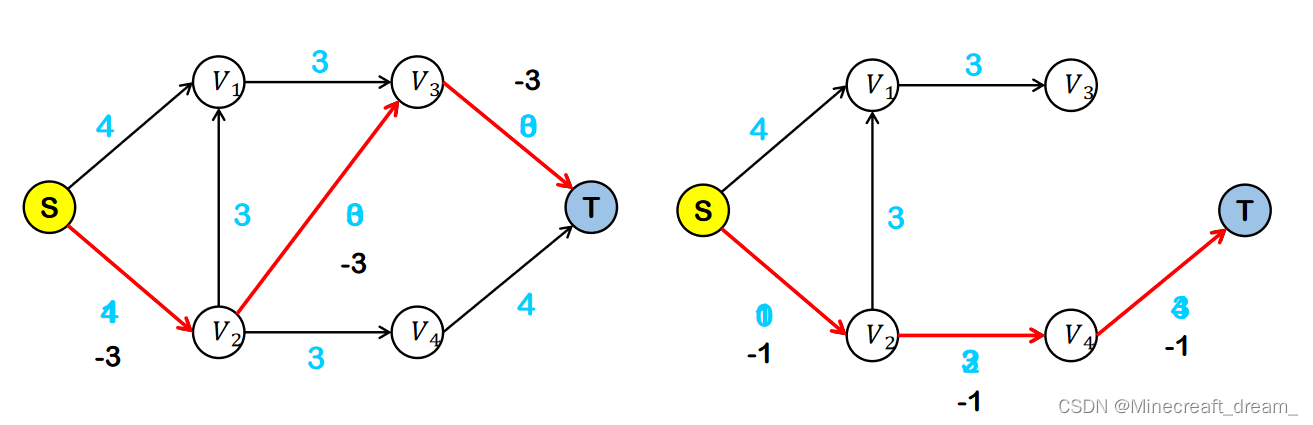
重复上述4步操作,直到图中不存在S->T的路径
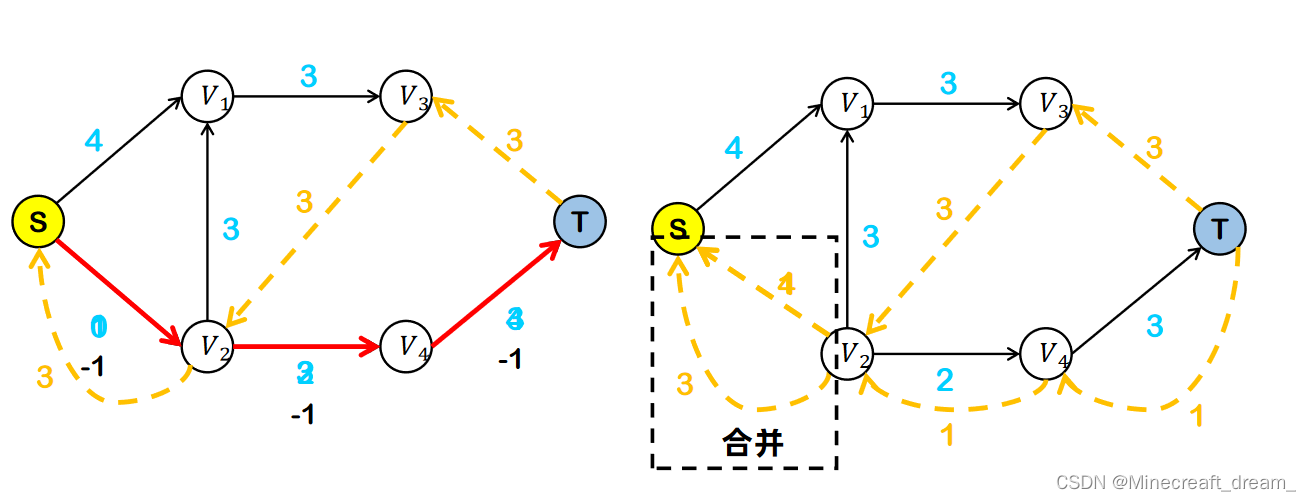
反向路径使得流量可以反悔回流。
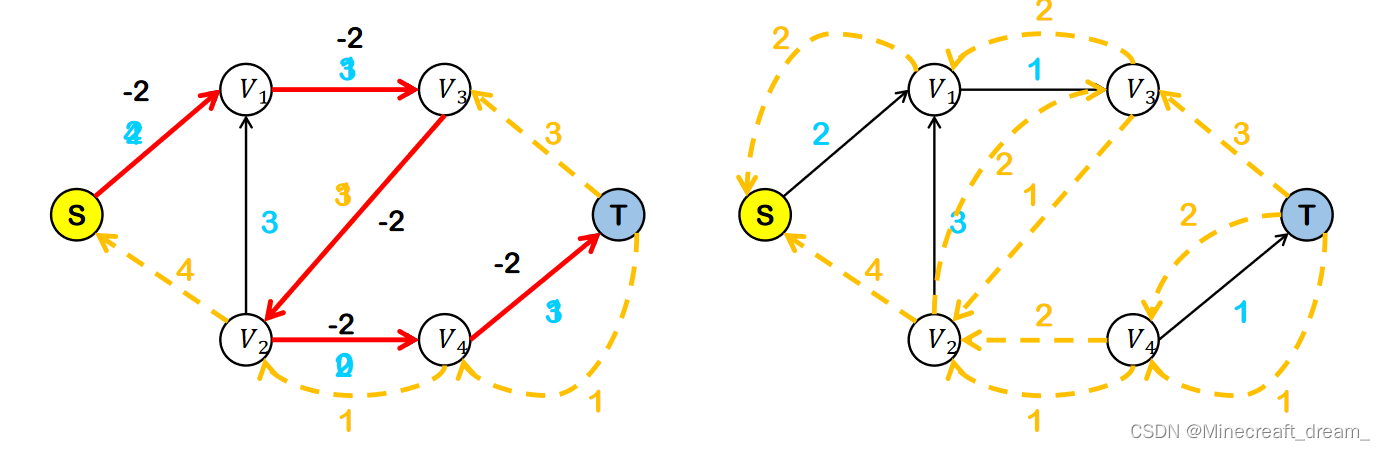
合并方向相同的边,不存在S->T的路径后删除反向路径。
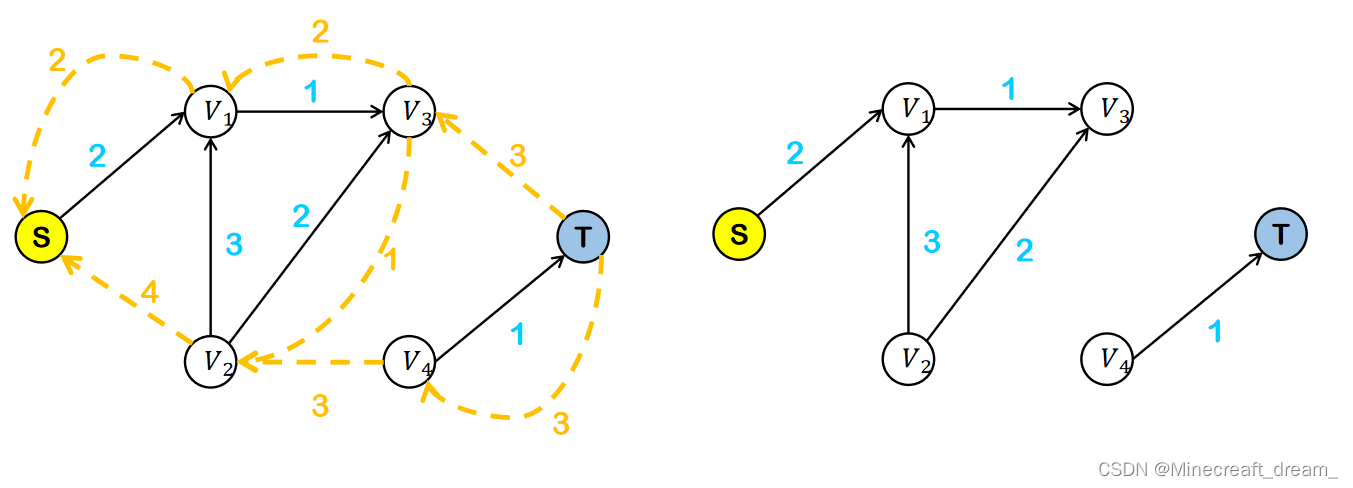
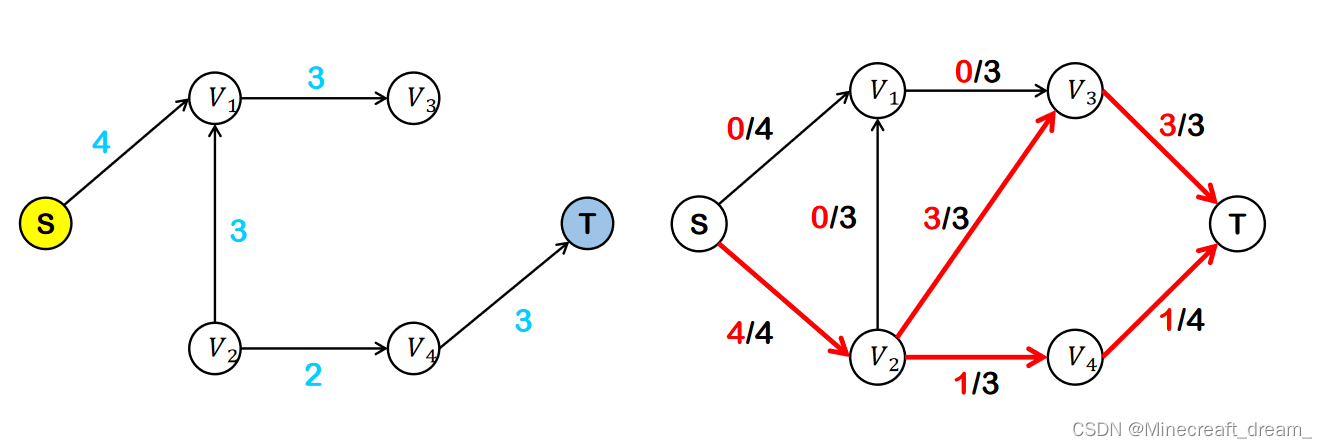
流量 = 容量 - 空闲量
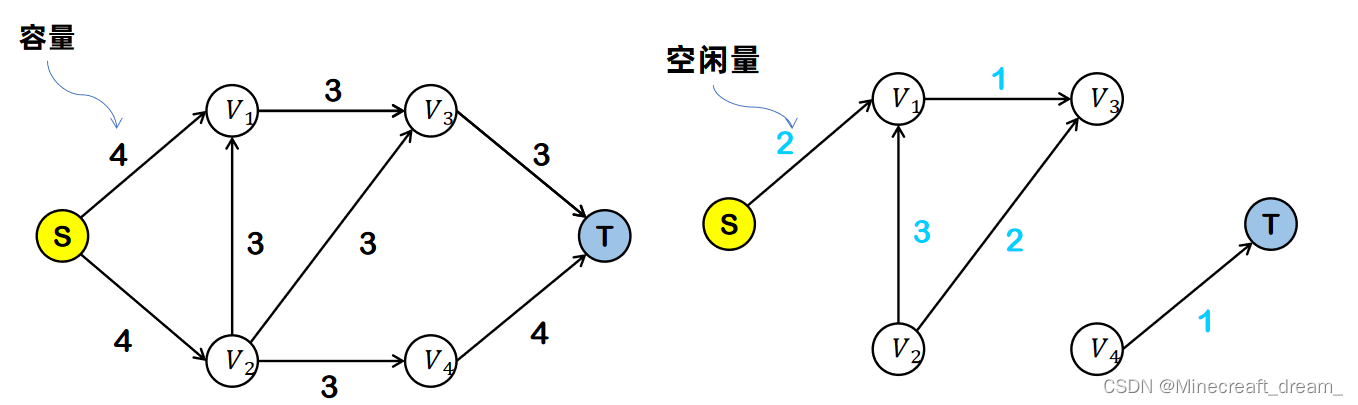
流量 = 容量 - 空闲量,最大流量 = 2 + 4 = 6。
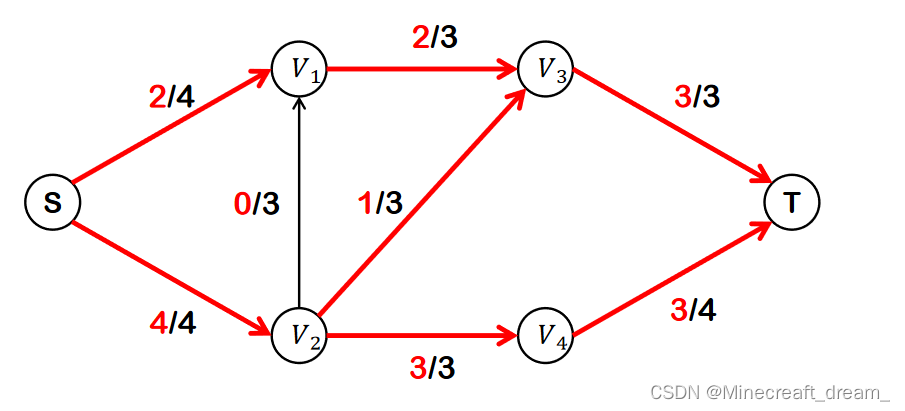
算法缺陷:ford-fulkerson算法在极端情况下时间复杂度非常糟糕。
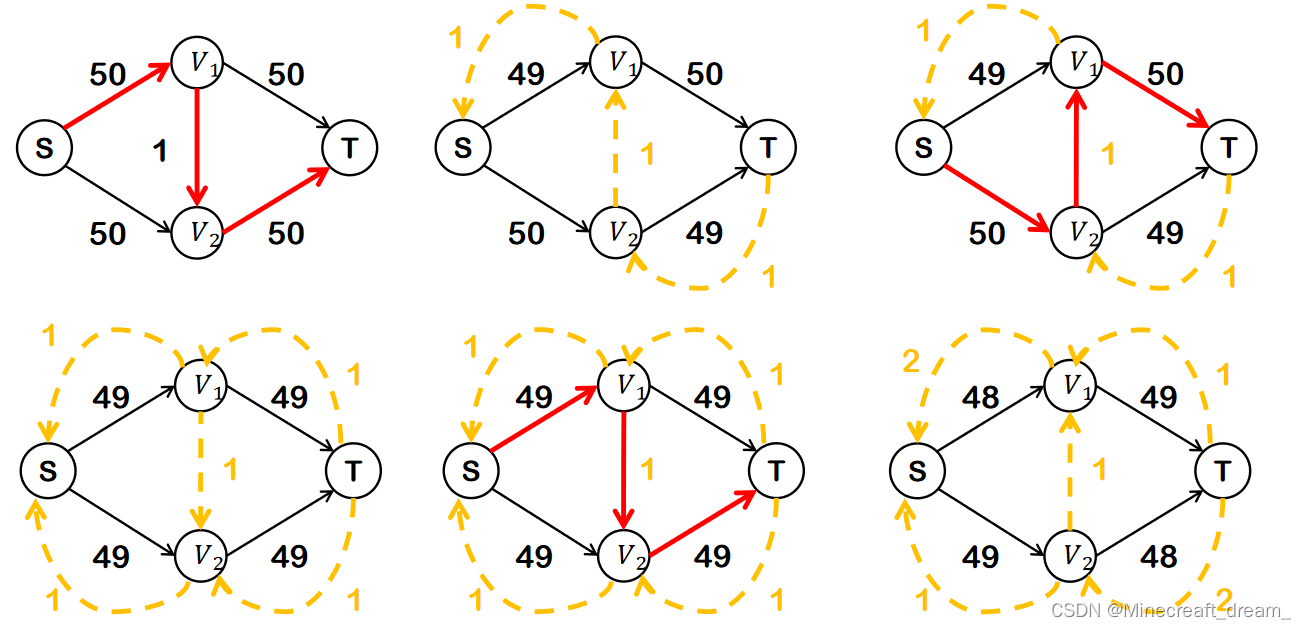
ford-fulkerson最坏情况下的重复次数等于最大流的大小。
设图中边的数量为M,单次查找路径的时间复杂度为O(M)
设流网络的最大流为F,则ford-fulkerson时间复杂度为O(F * M)。
2.Edmonds-Karp算法
2.1Edmonds-Karp算法流程
Edmonds-Karp算法是ford-fulkerson算法的性能优化算法,时间复杂度不依赖最大流的大小。
Edmonds-Karp算法每次找的路径都是S->T的最短路径,寻找最短路时将图当做无权图。
ford-fulkerson算法允许用任何的方式寻找S->T的路径,所以可以将Edmonds-Karp算法
看成ford-fulkerson算法的一种实现方式。 Edmonds-Karp算法的时间复杂度为






