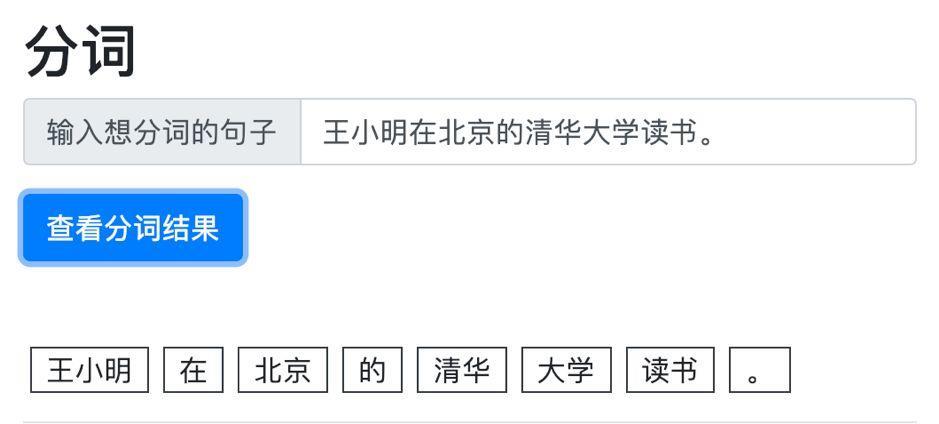
自然语言处理
朴素贝叶斯
贝叶斯定理
贝叶斯定理用来描述两个条件概率之间的关系,比如 P(A|B) 和 P(B|A)。按照乘法法则,可以立刻导出:P(A∩B) = P(A)*P(B|A)=P(B)*P(A|B)。如上公式也可变形为:P(B|A) = P(A|B)*P(B) / P(A)。
P(A)是A的先验概率或边缘概率。之所以称为”先验”是因为它不考虑任何B方面的因素。
P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
P(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
朴素贝叶斯分类
朴素贝叶斯是经典的机器学习算法之一,也是为数不多的基于概率论的分类算法。朴素贝叶斯原理简单,也很容易实现,多用于文本分类,比如垃圾邮件过滤。
朴素贝叶斯中的朴素一词的来源就是假设各特征之间相互独立。这一假设使得朴素贝叶斯算法变得简单,但有时会牺牲一定的分类准确率。
分类任务表达式:
P(类别|特征)= P(特征|类别)P(类别)/P(特征)
朴素贝叶斯分类器公式:

上式中分母对所有Ck都是相同的,故可以简化为:

朴素贝叶斯的优缺点:
优点:(1) 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
(2)分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点: 朴素贝叶斯假设属性之间相互独立,这种假设在实际过程中往往是不成立的。在属性之间相关性越大,分类误差也就越大。
sklearn中有3种不同类型的朴素贝叶斯:
高斯分布型:用于classification问题,假定属性/特征服从正态分布的。
多项式型:用于离散值模型里。比如文本分类问题里面我们提到过,我们不光看词语是否在文本中出现,也得看出现次数。如果总词数为n,出现词数为m的话,有点像掷骰子n次出现m次这个词的场景。
伯努利型:最后得到的特征只有0(没出现)和1(出现过)。
SVM
SVM介绍
支持向量机(support vector machines)是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。由简至繁的模型包括:
(1) 当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
(2) 当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
(3) 当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
线性分类器
如果一个线性函数能够将样本分开,称这些数据样本是线性可分的.线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线.间隔最大指一个点距离分离超平面的远近可以表示分类预测的确信度,如图中的A B两个样本点,B点被预测为正类的确信度要大于A点,所以SVM的目标是寻找一个超平面,使得离超平面较近的异类点之间能有更大的间隔,即不必考虑所有样本点,只需让求得的超平面使得离它近的点间隔最大。
即对于训练样本(xi,yi),满足以下公式:

该公式被称为最大间隔假设,yi=+1 表示样本为正样本,yi=−1 表示样本为负样本,SVM的思想是使得间隔最大化,也就是:

显然,最大化 2/||w|| 相当于最小化 ||w||,为了计算方便,将公式转化成如下公式,它即为支持向量机的基本型:

该基本型是一个凸二次规划问题,可以采用拉格朗日乘子法对其对偶问题求解求解.
SVM的文本分类过程
SVM 文本分类算法主要分四个步骤:文本特征提取、文本特征表示、归一化处理和文本分类。
(1)文本特征提取常采用特征独立性假设来简化特征选择的过程,达到计算时间和计算质量之间的折中。一般的方法是根据文本中词汇的特征向量,通过设置特征阀值的办法选择最佳特征作为文本特征子集,建立特征模型。(特征提取前,先分词,去停用词)。
本特征提取有很多方法,其中最常用的方法是通过词频选择特征。先通过词频计算出权重,按权重从大到小排序,然后剔除无用词,这些词通常是与主题无关的,一般在停词表中已定义好,去除这些词以后,有一个新的序列排下来,然后可以按照实际需求选取权重最高的前8个,10个或者更多词汇来代表该文本的核心内容。
(2)用tfidf计算权值来进行文本特征表示
(3)把需要处理的数据经过归一化处理后限制在需要的一定范围内。(4)经过文本预处理、特征提取、特征表示、归一化处理后,已经把原来的文本信息抽象成一个向量化的样本集,然后把此样本集与训练好的模板文件进行相似度计算,若不属于该类别,则与其他类别的模板文件进行计算,直到分进相应的类别,这就是SVM 模型的文本分类方式。
LDA主题模型
LDA基础
在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),他是一种处理文档的主题模型。
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想概括为“投影后类内方差最小,类间方差最大”。将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
LSA和PLSA
LSA(Latent Semantic Analysis)基本思想就是,将document从稀疏的高维Vocabulary空间映射到一个低维的向量空间.采用奇异值分解(Singular Value Decomposition)的方式来求解LSA。
LSA的优点:
(1)低维空间表示可以刻画同义词,同义词会对应着相同或相似的主题;
(2)降维可去除部分噪声,是特征更鲁棒;
(3)充分利用冗余数据;
(4)无监督/完全自动化;
(5)与语言无关;
LSA的缺点:
(1)没有刻画term出现次数的概率模型;
(2)无法解决多义词的问题;
(3)SVD的优化目标基于L-2 norm 或者是 Frobenius norm的,这相当于隐含了对数据的高斯噪声假设。而term出现的次数是非负的,这明显不符合Gaussian假设,而更接近Multi-nomial分布;
(4)对于count vectors 而言,欧式距离表达是不合适的(重建时会产生负数);
(5)特征向量的方向没有对应的物理解释;
(6)SVD的计算复杂度很高,而且当有新的文档来到时,若要更新模型需重新训练;
(7)维数的选择是ad-hoc的;
pLSA类似于LSA的思想,引入了一个Latent class,用概率模型的方式来表达LSA的问题.
pLSA的优点:
(1)定义了概率模型,而且每个变量以及相应的概率分布和条件概率分布都有明确的物理解释;
(2)相比于LSA隐含了高斯分布假设,pLSA隐含的Multi-nomial分布假设更符合文本特性;
(3)pLSA的优化目标是是KL-divergence最小,而不是依赖于最小均方误差等准则;
(4)可以利用各种model selection和complexity control准则来确定topic的维数;
pLSA的缺点:
(1)概率模型不够完备:在document层面上没有提供合适的概率模型,使得pLSA并不是完备的生成式模型,而必须在确定document i的情况下才能对模型进行随机抽样;
(2)随着document和term 个数的增加,pLSA模型也线性增加,变得越来越庞大;
(3)当一个新的document来到时,没有一个好的方式得到p(di);
(4)EM算法需要反复的迭代,需要很大计算量;