红黑树的本质是2-3-4树,所以我们先掌握了2-3-4树,那么红黑树就非常容易了。本文重点来介绍2-3-4树。
2-3-4树
1 概念介绍2-3-4树是四阶的 B树(Balance Tree),他属于一种多路查找树,它的结构有以下限制:
所有叶子节点都拥有相同的深度。节点只能是 2-节点、3-节点、4-节点之一。2-节点:包含 1 个元素的节点,有 2 个子节点;3-节点:包含 2 个元素的节点,有 3 个子节点;4-节点:包含 3 个元素的节点,有 4 个子节点;所有节点必须至少包含1个元素
元素始终保持排序顺序,整体上保持二叉查找树的性质,即父结点大于左子结点,小于右子结点;
而且结点有多个元素时,每个元素必须大于它左边的和它的左子树中元素。
下图是一个典型的 2-3-4树
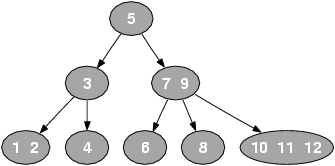
2 生成的过程
接下来我们通过演示来看看2-3-4树生成的过程第一次插入—2节点
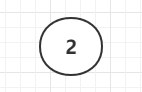
插入第二个节点–3节点 合并
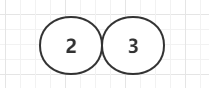
插入第三个节点—4节点 合并
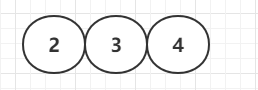
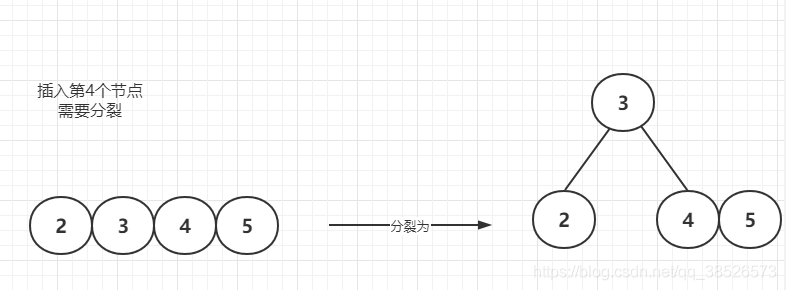
插入第4个节点—需要分裂
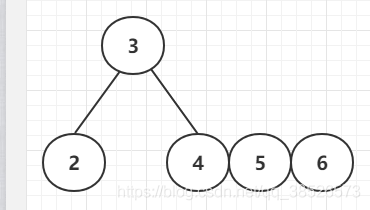
插入6
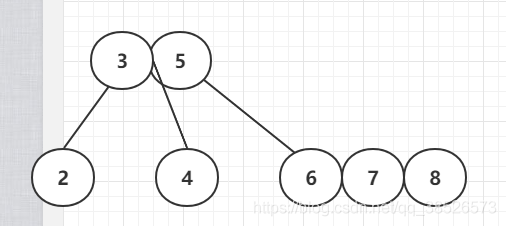
插入7

插入8
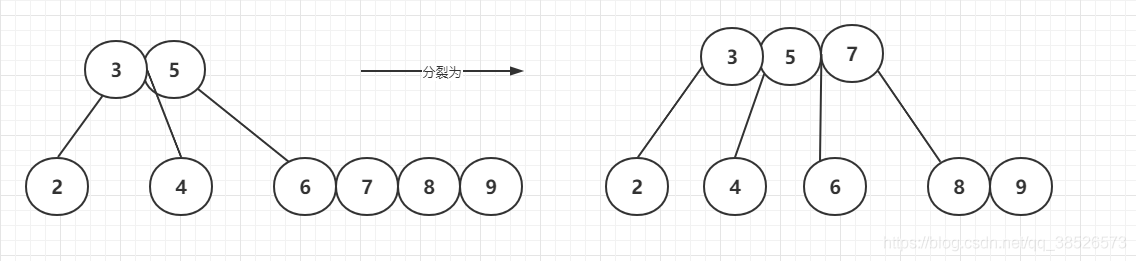
插入9
插入10
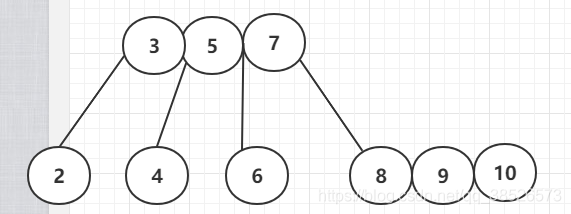
插入11
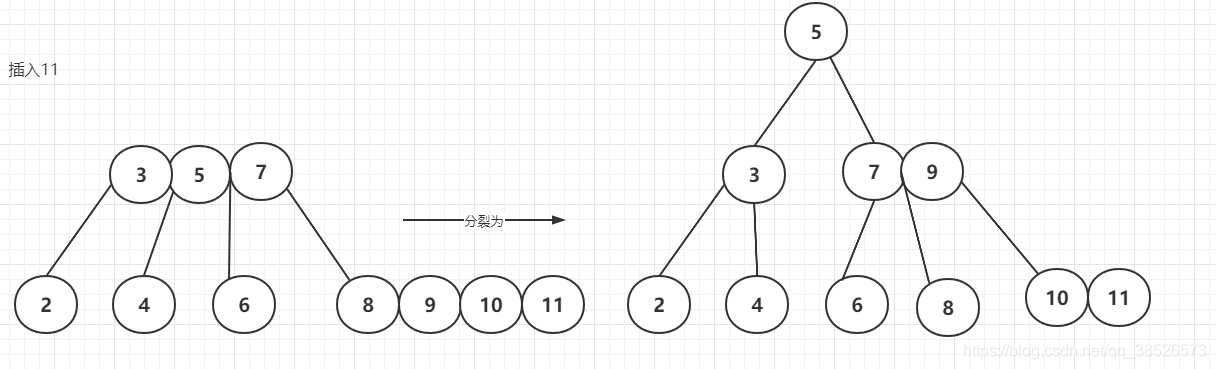
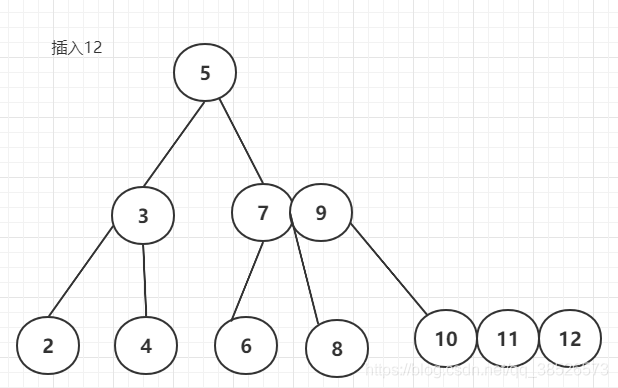
插入12
最后我们插入1来看看效果
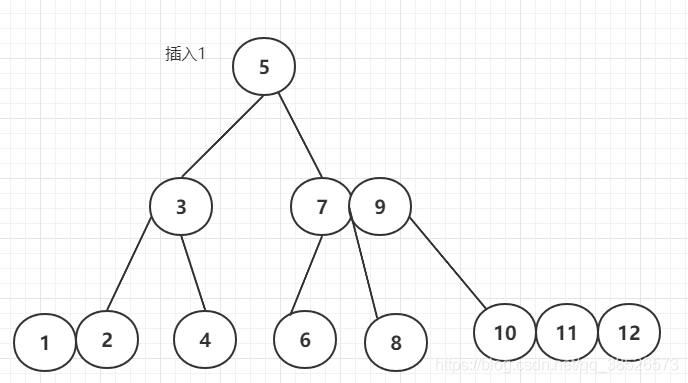
到这儿相信大家对于2-3-4树应该有了个直观的认知了。
3 和红黑树的等价关系
红黑树起源于2-3-4树,它的本质就是2-3-4树。3.1 2节点
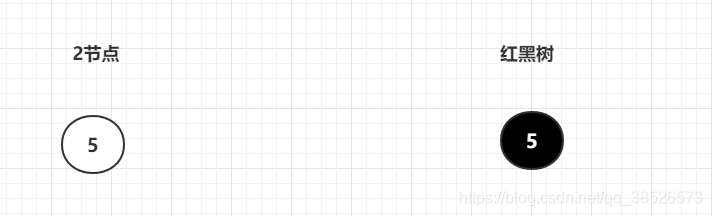
3.2 3节点
一个三节点可以有两种情况的红黑树节点,一种是右倾,一种是左倾,所以一个2-3-4树可以有多个红黑树
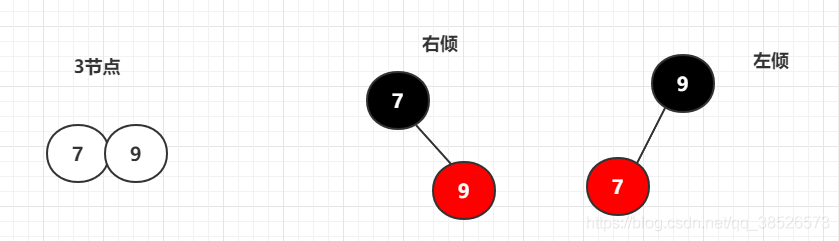
原则:上黑下红
3.3 4节点
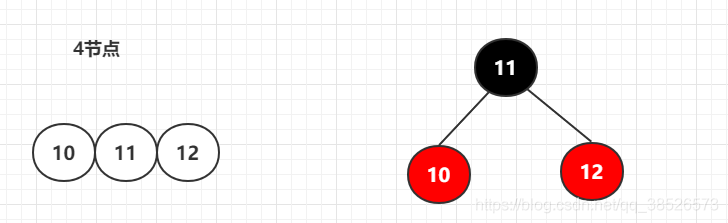
一个四节点转换的情况只有一种,中间节点黑色,左右节点红色
3.4 裂变状态
还有就是在2-3-4树中存在的裂变状态。转换为红黑树后会先变色(不能有两个相邻的红色节点)。
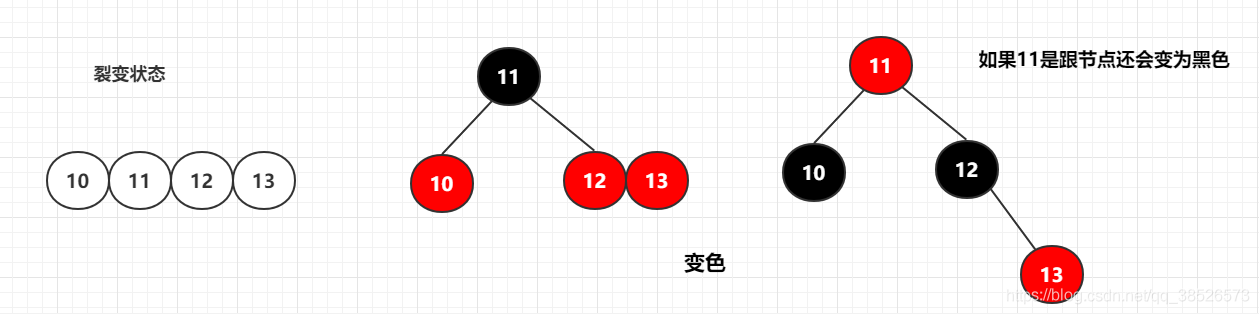
4 转换为红黑树
接下来具体看看一个2-3-4树是如何转换为对应的红黑树的,原始的2-3-4树:

按照右倾规则来转换为:
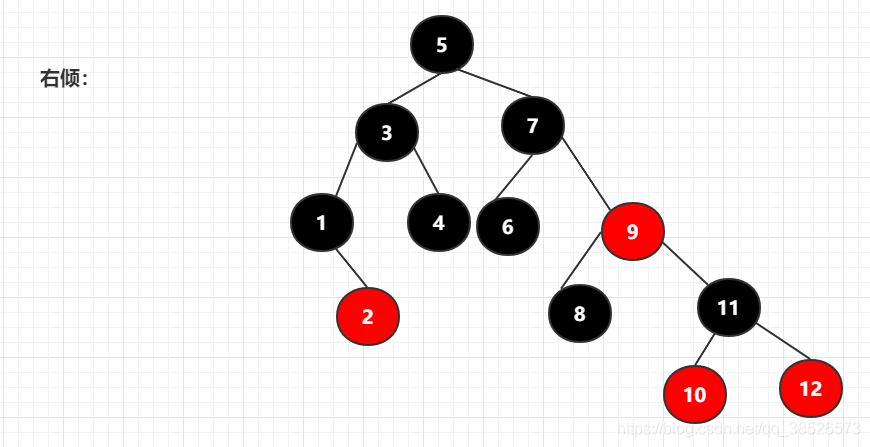
转换后满足黑色节点平衡的要求
按照左倾规则来转换为:

通过对2-3-4树和红黑树的等价关系,对于我们后面分析红黑树的内容会非常有帮助!!!






