【数据结构】证明法

反证法

• 基本概念：
  一般地，假设原命题不成立（即 在原命题的条件下，结论不成立），经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明原命题成立，这样的证明方法叫做反证法。

• 基本操作：
  1. 分清命题\(p=>q\)的条件和结论；
  2. 做出与命题结论\(q\)相矛盾的假定\(┐q\)；
  3. 由\(p\)和\(┐q\)出发，应用正确的推理方法，推出矛盾结果；

  4. 断定产生矛盾结果的原因，在于开始所作假定\(┐q\)不真，于是原结论\(q\)成立，从而间接地证明了命题\(p=>q\)为真。

     第三步所说的矛盾结果，通常是指推出的结果与已知条件、定义、定理或临时假定矛盾、以及自相矛盾等。

• 适用性：
  适用于“正难则反”的证明题
  凡是“至少”、“唯一”或含有否定词的命题适宜用反证法。

数学归纳法

• 基本概念：
  从初始情况，逐渐递推出n的结论。
• 基本步骤：
  一般地，证明一个与正整数n有关的命题，可按下列步骤进行：
  1. （归纳奠基）证明当n取第一个值\(n_0\)时命题成立；
  2. （归纳递推）假设n=k(k≥\(n_0\))时命题成立，证明当n=k+1时命题也成立。
     只要完成上面两个步骤，即可断定（递推出）命题从\(n_0\)开始的所有正整数n都成立。
• 格式：
  1. 当n=1时,显然成立.
  2. 假设当n=k时（把式中n换成k,写出来）成立,
  3. 则，当n=k+1时,（这步比较困难,化简步骤往往繁琐,考试时可以直接写结果)该式也成立.
  4. 由（1）（2）得,原命题对任意正整数均成立，原命题成立。
• 注意：
  用数学归纳法证明命题时，需注意：
  1. 第一步是基础，首先要验证n=\(n_0\)时成立，注意\(n_0\)不一定为1；
  2. 第二步是依据，在第二步中，关键是要正确合理地运用归纳假设，尤其要弄清k到k+1的变化，两个步骤缺一不可，且书写必须规范。
• 适用性：
  只适用于与正整数n有关的命题的证明方法
• 补充：
  用数学归纳法还可以解决数列中的归纳猜想问题，基本步骤是：观察、归纳、猜想、证明，一般要根据已知条件和递推关系，先求出数列的前几项，然后总结归纳其中的规律，猜想结论，再利用数学归纳法证明。猜想是证明的前提和对象，因此务必保持猜想的正确性，同时注意数学归纳法的书写步骤。

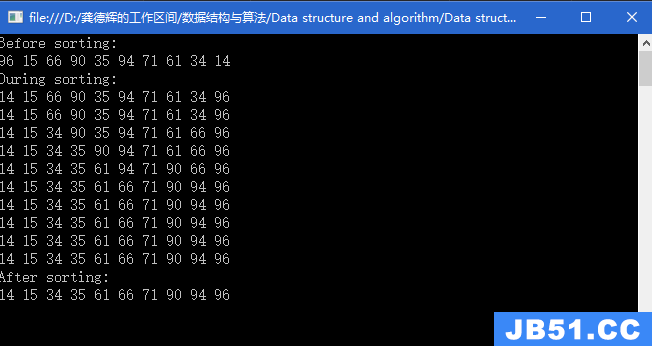
综合例题

证明 n 个节点的无向连通图最少有 n-1 条边。

• 数学归纳法：
  1. 当n=1时，最少有0条边，显然成立；
  2. 假设当n=k(k≥1)时，最少有k-1条边，命题成立，则
  3. 当n=k+1时，图中分为两部分，一部分为k个结点最少有k-1条边，第二部分为一个单独的结点，若其需与其他结点相连通，得添加一条边，故最少有(k-1)+1=k条边。
  4. 故原命题成立。

设图G有n个结点，n＋1条边，证明：G中至少有1个结点度数大于等于3。

• 反证法： 
  1. 假设G=<V,E>，任意v∈V，deg(v)≤2。所有结点的度数之和2(n+1)小于2n。
  2. 即2(n+1)≤2n，化简后，2≤0，矛盾。 
  3. 故G中至少有1个结点度数大于等于3。

设无向图G有9个结点，每个结点的度数不是5就是6，证明：G中至少有5个6度结点或至少有6个5度结点。

• 反证法：
  1. 假设6度结点小于5个且5度结点小于6个，则只可能有5个5度结点，4个6度结点(其他情况结点数的和小于9)。
  2. 此时，各结点度数之和为：5×5+4×6=25+24=49。与结点度数之和为偶数(边数两倍)矛盾。 
  3. 故G中至少有5个6度结点或至少有6个5度结点。