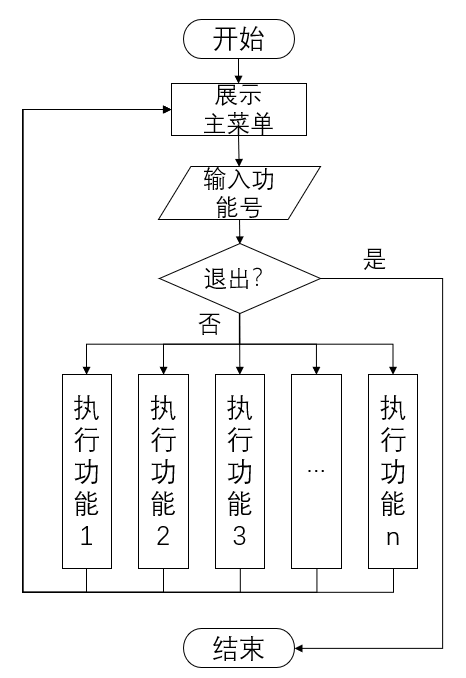
是否有任何已知的方法可以快速有效地确定3D点是否位于已知大小的柏拉图体积内?
这对于立方体(六面体)或圆形(椭圆体)来说似乎很容易.我似乎无法弄清楚四面体,八面体,十二面体还是二十面体.我猜测可能会将形状分解为几个子实体,然后检查每个子实体,但是如果可能的话,我想避免任何类型的迭代求解器.
解决方法
一种简单的方法是将实体表示为半空间的交集.
3d中的平面具有隐式方程:
ax + by + cz + d = 0
其中(a,b,c)是平面法线,d是平面任意点的 – (a * x b * y c * z)的值(计算值不取决于您选择的点).
对于平面一侧的空间中的点,* x b * y c * z d的结果将为负,而另一方面,结果将为正.
柏拉图实体(任何凸实体)可以表示为所有面的非正面上的空间点,即
a[i]*x + b[i]*y + c[i]*z + d[i] <= 0
因此,一个相当快的测试可能是:
struct Plane {
double a,c,d;
};
struct Point {
double x,y,z;
};
int side(const Point pt,const Plane& pl) {
double v = pt.x*pl.a + pt.y*pl.b + pt.z*pl.c + pl.d;
if (v < -EPS) return -1;
if (v > EPS) return 1;
return 0;
}
struct ConvexSolid {
std::vector<Plane> planes;
bool contains(const Point& pt) const {
return std::all_of(planes.begin(),planes.end(),[&](const Plane& pl){
return side(pt,pl) <= 0;
});
}
};