递归

递归实现的原理：对于递归的问题，我们一般都是从上往下递归的，直到递归到最底，再一层一层着把值返回。
一个递归函数的调用过程类似于多个函数的嵌套的调用，只不过调用函数和被调用函数是同一个函数。为了保证递归函数的正确执行，系统需设立一个工作栈。具体地说，递归调用的内部执行过程如下：

运动开始时，首先为递归调用建立一个工作栈，其结构包括值参、局部变量和返回地址；
每次执行递归调用之前，把递归函数的值参、局部变量的当前值以及调用后的返回地址压栈；
每次递归调用结束后，将栈顶元素出栈，使相应的值参和局部变量恢复为调用前的值，然后转向返回地址指定的位置继续执行。

在我们了解了递归的基本思想及其数学模型之后，我们如何才能写出一个漂亮的递归程序呢？我认为主要是把握好如下三个方面：

明确递归函数的作用；
明确递归终止条件与对应的解决办法；
找出函数的等价关系式，提取重复的逻辑缩小问题规模。

递归三步走

递归三步走：

明确函数功能：要清楚你写这个函数是想要做什么；
寻找递归出口：递归一定要有结束条件，不然会永远递归下去，禁止套娃；
找出递推关系：开始实现递归，一步一步递推出最终结果。

明确函数功能

第一步，明确这个函数的功能是什么，它要完成什么样的一件事。
而这个功能，是完全由你自己来定义的。也就是说，我们先不管函数里面的代码是什么、怎么写，而首先要明白，你这个函数是要用来干什么的。

例如：求解任意一个数的阶乘
要做出这个题，
第一步，要明确即将要写出的这个函数的功能为：算n的阶乘。

//算n的阶乘（假设n不为0）
int f(int n) {
    
}

寻找递归出口（初始条件）

递归就是在函数实现的内部代码中，调用这个函数本身。所以，我们必须要找出递归的结束条件，不然的话，会一直调用自己，一直套娃，直到内存充满。

必须有一个明确的结束条件。因为递归就是有“递”有“归”，所以必须又有一个明确的点，到了这个点，就不用“递下去”，而是开始“归来”。

第二步，我们需要找出当参数为何值时，递归结束，之后直接把结果返回。
（一般为初始条件，然后从初始条件一步一步扩充到最终结果）

注意：这个时候我们必须能根据这个参数的值，能够直接知道函数的结果是什么。

让我们继续完善上面那个阶乘函数。
第二步，寻找递归出口：
当n=1时，我们能够直接知道f(1)=1；
那么递归出口就是n=1时函数返回1。
如下：

//算n的阶乘（假设n不为0）
int f(int n) {
    if(n == 1) {
        return 1;
    }
}

当然，当n=2时，我们也是知道f(2)等于多少的，n=2也可以作为递归出口。递归出口可能并不唯一的。

找出递推关系

第三步，我们要从初始条件一步一步递推到最终结果。

类比：数学归纳法，多米诺骨牌

初始条件：f(1) = 1
递推关系式：f(n) = f(n-1)*n

递归：

递：f(n) = n * f(n-1)，将f(n)→f(n-1)了。这样，问题就由n缩小为了n-1，并且为了原函数f(n)不变，我们需要让f(n-1)乘以n。就这样慢慢从f(n),f(n-1)“递”到f(1)。
归：这样就可以从n=1，一步一步“归”到n=2,n=3...

// 算n的阶乘（假设n不为0）
int f(int n) {
    if(n = 1) {
        return n;
    }
    // 把f(n)的递推关系写进去
    return f(n-1) * n;
}

到这里，递归三步走就完成了，那么这个递归函数的功能我们也就实现了。
可能初学的读者会感觉很奇妙，这就能算出阶乘了？
那么，我们来一步一步推一下。
f(1)=1
f(2)=f(1)*2=2
f(3)=f(2)*3=2*3=6
...
你看看是不是解决了，n都能递推出来！

实例

斐波那契数列

斐波那契数列的是这样一个数列：1、1、2、3、5、8、13、21、34....，即第一项 f(1) = 1,第二项 f(2) = 1.....,第 n 项目为 f(n) = f(n-1) + f(n-2)。求第 n 项的值是多少。

明确函数功能：f(n)为求第n项的值

// 1.f(n)为求第n项的值
int f(int n) {

}

寻找递归出口：f(1)=1,f(2)=1

// 1.f(n)为求第n项的值
int f(int n) {
    // 2.递归出口
    if(n <= 2) {
        return 1;
    }
}

找出递推关系：f(n) = f(n-1) + f(n-2)

// 1.f(n)为求第n项的值
int f(int n) {
    // 2.递归出口
    if(n <= 2) {
        return 1;
    }
    // 3.递推关系
    return f(n-1) + f(n-2);
}

小青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

明确函数功能：f(n)为青蛙跳上一个n级的台阶总共有多少种跳法
```
int f(int n) {

}
```

寻找递归出口：f(0)=0,f(1)=1

int f(int n) {
    // 递归出口
    if(n <= 1) {
        return n;
    }
}

找出递推关系：f(n) = f(n-1)+f(n-2)

int f(int n) {
    // 递归出口
    if(n <= 2) {
        return 1;
    }
    // 递推关系
    return f(n-1) + f(n-2);
}

优化思路

重复计算

其实递归当中有很多子问题被重复计算。

对于斐波那契数列，f(n) = f(n-1)+f(n-2)。
递归调用的状态图如下：

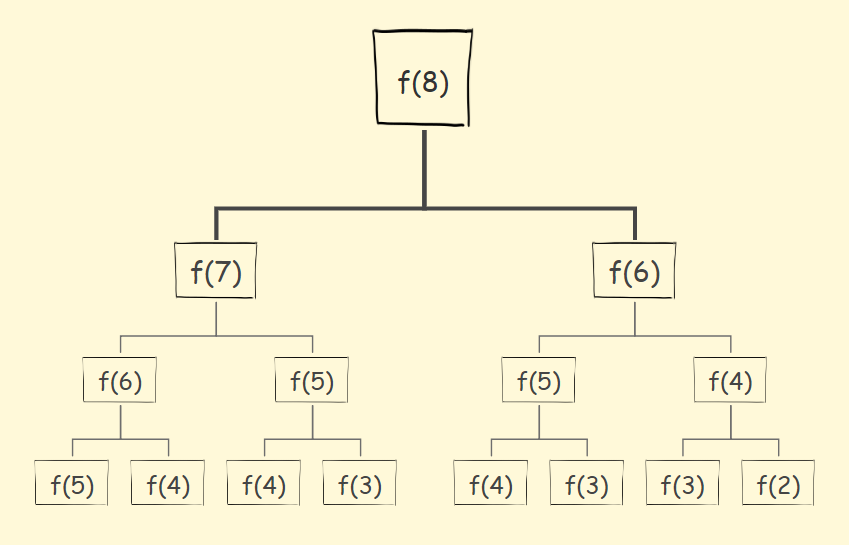
其中，递归计算时f(6)、f(5)...都被重复了很多次，这是极大的浪费，当n越大，因重复计算浪费的就越多，所以我们必须要进行优化。

优化思路：
- 建立一个数组，将子问题的计算结果保存起来。
- 判断之前是否计算过：
  - 计算过，取出来用
  - 没有计算过，再递归计算
实例：
- 把n作为数组下标，f(n)作为值。
  例如arr[n] = f(n)。
- f(n)还没有计算过的时候，我们让arr[n]等于一个特殊值。
  例如arr[n] = -1。
- 当我们要判断的时候，
  - 如果 arr[n] = -1，则证明f(n)没有计算过；
  - 否则，f(n)就已经计算过了，且f(n) = arr[n]。
    直接把值取出来用就行了。

代码如下：

// 我们实现假定 arr 数组已经初始化好的了。
int f(int n) {
    if(n <= 1) {
        return n;
    }
    //先判断有没计算过
    if(arr[n] != -1) {
        //计算过，直接返回
        return arr[n];
    }else {
        // 没有计算过，递归计算,并且把结果保存到 arr数组里
        arr[n] = f(n-1) + f(n-1);
        reutrn arr[n];
    }
}

剪枝

剪枝：就是在算法优化中，通过某种判断，避免一些不必要的遍历过程。
形象的说，就是剪去了搜索树中的某些“枝条”，故称剪枝。
应用剪枝优化的核心问题是设计剪枝判断方法，即确定哪些枝条应当舍弃，哪些枝条应当保留的方法。

类比：这个剪枝其实就像人生，一个人因很多种选择，而到达不同的结局，然而有些选择我们一开始就可以判断是bad end了，那么我们在一开始就不会选择那样的道路，而不是到达结局才发现是bad end，撞了南墙才知道疼。
未剪枝——不撞南墙不死心，到最后结局才能判断是否是自己想要的结果
剪枝——及时止损

剪枝可分为：

可行性剪枝
最优性剪枝

可行性剪枝

可行性剪枝：该方法判断继续搜索能否得出答案，如果不能直接回溯。

最优性剪枝

最优性剪枝：又称为上下界剪枝，是一种重要的搜索剪枝策略。
它记录当前得到的最优值，如果当前结点已经无法产生比当前最优解更优的解时，可以提前回溯。

自底向上

上面说了那么多，都是自顶向下（把问题逐步变小）的递归。
（但是我比较习惯按自顶向下做，按自底向上思考递归，因为比较符合数学归纳法，顺着推）

除了自顶向下，其实自底向上也是可以完成任务的！
例如，上面的斐波那契数列
自顶向下：把问题逐渐减小

int Fibonacci(int n) {
    if(n == 0)
        return 0;
    if(n == 1)
        return 1;
    return Fibonacci(n-1) + Fibonacci(n-2);
}

自底向上：用底部的小问题答案，组装成最后的大问题答案

int Fibonacci(int n) {
    int array[n] = {0};
    array[1] = 1;
    for(int i = 2; i < n; i++)
        array[i] = array[i-1] + array[i-2];
}

【算法】递归三步走

递归